
【题目】已知函数![]() ,对于
,对于![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先分析得到函数f(x)在[0,2]上单调递增,再转化得到0≤![]() ≤1恒成立,分析解答两个不等式恒成立问题即得解.
≤1恒成立,分析解答两个不等式恒成立问题即得解.
由题得当![]() 时,
时,![]() ,
,
所以![]() ,
,
所以函数f(x)在[0,2]上单调递增,
因为f(1)=4+cosπ=3,
所以![]() f(1),
f(1),
所以![]() ≤1,
≤1,
因为![]() ≤1且0≤
≤1且0≤![]() ≤2
≤2
所以0≤![]() ≤1.
≤1.
当![]() ≤1时,
≤1时,
所以![]() ,当x=0时,显然成立.
,当x=0时,显然成立.
当0<x≤2时,![]()
![]() ,
,
所以g(x)在(1,2)单调递增,在(0,1)单调递减,
所以![]() ,所以
,所以![]() .
.
当![]() ≥0时,
≥0时,![]() ,
,
当x=0时,显然成立.
当0<x≤2时,![]() ,
,
令![]() ,
,
所以k(x)在(0,2)单调递增,所以k(x)>k(0)=0,
所以函数![]()
所以函数h(x)在(0,2]上单调递增,
所以h(x)最大值=h(2)=![]() .
.
所以![]() .
.
综上得![]() .
.
故选:B


科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
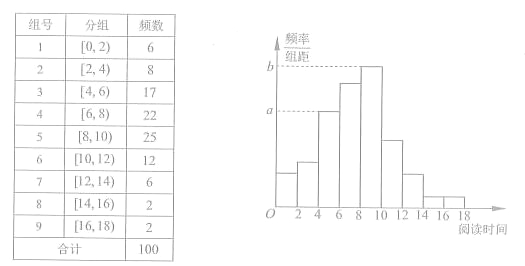
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某地区积极践行“绿水青山就是金山银山”的绿色发展理念![]() 年年初至
年年初至![]() 年年初,该地区绿化面积
年年初,该地区绿化面积![]() (单位:平方公里)的数据如下表:
(单位:平方公里)的数据如下表:
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测该地区![]() 年年初的绿化面积,并计算
年年初的绿化面积,并计算![]() 年年初至
年年初至![]() 年年初,该地区绿化面积的年平均增长率约为多少.
年年初,该地区绿化面积的年平均增长率约为多少.
(附:回归直线的斜率与截距的最小二乘法估计公式分别为 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在乎面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴的非负半轴为极轴,且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴,且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,E是
,E是![]() 中点,M是
中点,M是![]() 的中点,F是
的中点,F是![]() 上的动点.
上的动点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,当F是
,当F是![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,动点
,动点![]() ,线段
,线段![]() 与圆
与圆![]() 相交于点
相交于点![]() ,线段
,线段![]() 的长度与点
的长度与点![]() 到
到![]() 轴的距离相等.
轴的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交圆
两点,交圆![]() 于
于![]() ,
,![]() 两点,其中
两点,其中![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com