
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.
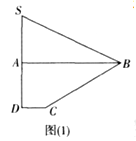
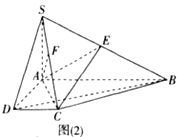
(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M,N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里, ![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位
(单位![]() )的情况如下表1:
)的情况如下表1:
![]()
哈尔滨市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
![]()
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式: ![]() ,其中
,其中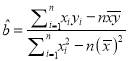 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于200时,洗车店平均每天亏损约2000元;当
不高于200时,洗车店平均每天亏损约2000元;当![]() 在
在![]() 时,洗车店平均每天收入约4000元;当
时,洗车店平均每天收入约4000元;当![]() 大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0
(1)求函数f(x)的解析式;
(2)若a>0,解关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com