
| A. | 8 | B. | $4\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
分析 求出抛物线的焦点为F(2,0),直线的斜率k=tan60°=$\sqrt{3}$,从而得到直线的方程.直线方程与抛物线方程联解消去y得3x2-20x+12=0,利用根与系数的关系可得x1+x2=$\frac{20}{3}$,再根据抛物线的定义加以计算,即可得到直线被抛物线截得的弦长.
解答 解:∵抛物线方程为y2=8x,2p=8,$\frac{p}{2}$=2,∴抛物线的焦点是F(2,0).
∵直线的倾斜角为60°,∴直线斜率为k=tan60°=$\sqrt{3}$
可得直线方程为:y=$\sqrt{3}$(x-2),
设直线交抛物线于点A(x1,y1),B(x2,y2),
联解,消去y得3x2-20x+12=0,
∴x1+x2=$\frac{20}{3}$,
根据抛物线的定义,可得|AF|=x1+$\frac{p}{2}$=x1+2,|BF|=x2+$\frac{p}{2}$=x2+2,
∴|AB|=x1+x2+4=$\frac{32}{3}$,即直线被抛物线截得的弦长为$\frac{32}{3}$.
故选:D.
点评 本题给出经过抛物线的焦点的直线倾斜角为60°,求直线被抛物线截得的弦长.着重考查了抛物线的定义与标准方程、一元二次方程根与系数的关系、直线与圆锥曲线的位置关系等知识,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0)的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率e=$\frac{\sqrt{3}}{2}$,△DEF2的面积为1-$\frac{\sqrt{3}}{2}$.若M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知OP⊥OQ.
如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0)的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率e=$\frac{\sqrt{3}}{2}$,△DEF2的面积为1-$\frac{\sqrt{3}}{2}$.若M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知OP⊥OQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
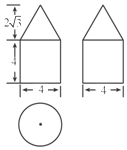 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )
如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的体积为( )| A. | 16π+$\sqrt{3}π$ | B. | 16π+8$\sqrt{3}$π | C. | 16π+$\frac{8}{3}\sqrt{3}π$ | D. | 16π+$\frac{4}{3}\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,AB=1,$AD=\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD.
如图,四边形ABCD是矩形,AB=1,$AD=\sqrt{2}$,E是AD的中点,BE与AC交于点F,GF⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com