
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
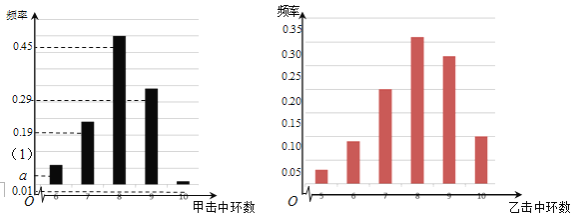
(1)求上图中![]() 的值;
的值;
(2)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(3)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(Ⅰ)根据题意建立的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
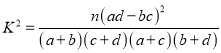 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)求证: ![]() 不是
不是![]() 上的奇函数;
上的奇函数;
(2)若![]() 是
是![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的值;
的值;
(3)若函数![]() 在区间
在区间![]() 上恰有3个不同的零点,求实数
上恰有3个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
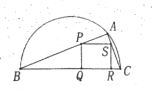
【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com