
| A、命题“若x>y,则x2>y2的否命题为“若x>y,则x2≤y2” |
| B、命题p:“?x>0,sinx<x”.则¬p:“?x<0,sinx≥x” |
| C、“x<0”是“ln(x+1)<0”的必要不充分条件 |
| D、命题p:f(x)=xsinx为奇函数,命题q:f(x)=cosx+1为偶函数,则“p∨q”为假命题 |


科目:高中数学 来源: 题型:
| A、老年人应作为重点调查对象,故老年人应该抽超过30名 | ||
B、每个人被抽到的概率相同为
| ||
| C、应使用分层抽样抽取样本调查 | ||
| D、抽出的样本能在一定程度上反应总体的健康状况 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
| B、2 | ||
C、
| ||
| D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
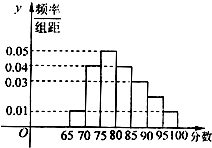 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
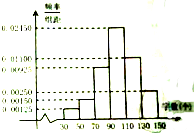 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.| 1 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com