
分析 (1)对函数f(x)求导,利用函数的导函数与极值的关系,令导函数等于0即可解出m的值.
(2)根据导数和函数最值的关系即可求出函数的值域.
解答 解:(1)∵f′(x)=(x-m)2+2x(x-m)=3x2-4mx+m2,且f(x)=x(x-m)2+1(m∈R)在x=1处有极大值,
∴f′(1)=0,即m2-4m+3=0,解得m=1或3.
经检验m=1时,函数f(x)在x=1处取得极小值,不符合题意,应舍去.
故m=3.
(2)由(1)知f′(x)=3x2-12x+9,令f′(x)=0,解得x=1或x=3,
当f′(x)>0时,即$\frac{1}{2}$≤x<1,或3<x≤5,函数f(x)为增函数,
当f′(x)>0时,即1<x<3,函数f(x)为减函数,
f($\frac{1}{2}$)=$\frac{33}{8}$,f(3)=1,f(1)=5,f(5)=21,
∴f(x)在区间[$\frac{1}{2}$,5]上的值域为[1,21]
点评 本题考查了导数和函数的极值和最值的关系,关键是判断函数的单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题. | D. | ①是假命题,②是真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
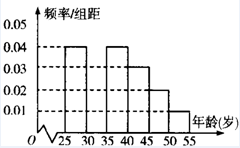 某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行
某班同学在暑假期间进行社会实践活动,从本地[25,55]岁的人群中随机抽取n人进行| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | P |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com