
【题目】已知椭圆中心在坐标原点O,焦点在![]() 轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线
轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线![]() 平行OM,且与椭圆交于A、B两个不同的点。
平行OM,且与椭圆交于A、B两个不同的点。
(Ⅰ)求椭圆方程;
(Ⅱ)若![]() AOB为钝角,求直线
AOB为钝角,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围;
的取值范围;
(Ⅲ)求证直线MA、MB与![]() 轴围成的三角形总是等腰三角形。
轴围成的三角形总是等腰三角形。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】试题分析:(1)设椭圆方程![]() ,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;(2)设l方程与椭圆方程联立,利用韦达定理及∠AOB为钝角,结合向量知识,即可求直线l在y轴上的截距m的取值范围;(3)依题即证kAM+kBM=0,利用韦达定理代入,即可证得结论.
,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;(2)设l方程与椭圆方程联立,利用韦达定理及∠AOB为钝角,结合向量知识,即可求直线l在y轴上的截距m的取值范围;(3)依题即证kAM+kBM=0,利用韦达定理代入,即可证得结论.
解析:
(1)解:设椭圆方程![]() ,依题意可得可得
,依题意可得可得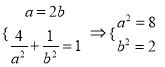 所以椭圆方程为
所以椭圆方程为![]()
(2)解:设l方程为: ![]() 与椭圆方程联立得:x2+2mx+2m2﹣4=0
与椭圆方程联立得:x2+2mx+2m2﹣4=0
由韦达定理得:x1+x2=﹣2m, ![]() ;
;
设A(x1,y1),B(x2,y2),
因为∠AOB为钝角,所以![]()
![]()
又直线l平行OM, ![]()
(3)证明:依题即证kAM+kBM=0
![]()
将直线代入上式得到,得![]()
韦达定理代入得,上式=0.得证。


科目:高中数学 来源: 题型:
【题目】定义:max{a,b}= ![]() ,若实数x,y满足:|x|≤3,|y|≤3,﹣4x≤y≤
,若实数x,y满足:|x|≤3,|y|≤3,﹣4x≤y≤ ![]() x,则max{|3x﹣y|,x+2y}的取值范围是( )
x,则max{|3x﹣y|,x+2y}的取值范围是( )
A.[ ![]() ,7]
,7]
B.[0,12]
C.[3, ![]() ]
]
D.[0,7]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点
的顶点在原点![]() ,对称轴是
,对称轴是![]() 轴,且过点
轴,且过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,
轴, ![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,判断点
,判断点![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4![]() ,半径小于5.
,半径小于5.
(Ⅰ)求直线PQ与圆C的方程;
(Ⅱ)若直线l∥PQ,直线l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右焦点为
的右焦点为![]() ,
, ![]() 是双曲线C上的点,
是双曲线C上的点, ![]() ,连接
,连接![]() 并延长
并延长![]() 交双曲线C与点P,连接
交双曲线C与点P,连接![]() ,若
,若![]() 是以
是以![]() 为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
为顶点的等腰直角三角形,则双曲线C的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 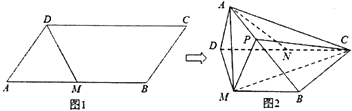
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在约束条件 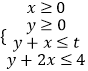 下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
A.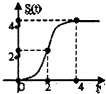
B.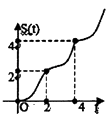
C.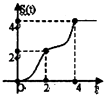
D.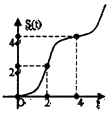
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司引进一条价值30万元的产品生产线,经过预测和计算,得到生产成本降低![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间满足:①
万元之间满足:①![]() 与
与![]() 和
和![]() 的乘积成正比;②当
的乘积成正比;②当![]() 时,
时, ![]() ,并且技术改造投入比率
,并且技术改造投入比率![]() ,
, ![]() 为常数且
为常数且![]() .
.
(1)求![]() 的解析式及其定义域;
的解析式及其定义域;
(2)求![]() 的最大值及相应的
的最大值及相应的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com