
【题目】已知正项数列{an},其前n项和Sn满足6Sn=an2+3an+2,且a1 , a2 , a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1b1+a2b2+…+anbn , n∈N*,求Tn .
【答案】
(1)解:由题意得:因为6Sn=an2+3an+2①,所以6Sn﹣1=an﹣12+3an﹣1+2②,
所以②﹣①得:6Sn﹣6Sn﹣1=an2+3an+2﹣an﹣12+3an﹣1+2,
所以3an+3an﹣1=(an+an﹣1)(an﹣an﹣1),
又因为正项数列{an},所以an+an﹣1>0,
所以an﹣an﹣1=3,
当n=1时,6S1=a12+3a1+2,
所以a1=1或2,
又因为a1=2时,a2=2+3=5,a6=2+5*3=17,显然a1,a2,a6不是等比数列,
所以a1=1,
所以an=a1+(n﹣1)d=3n﹣2;
又因为a1,a2,a6是等比数列{bn}的前三项,
所以a2=4,a6=16,
所以q=4,
所以bn}=a1*qn﹣1=4n﹣1
(2)解:由(1)可知anbn=(3n﹣2)*4n﹣1,
所以Tn=a1b1+a2b2+…+an﹣1bn﹣1+anbn=1*41+4*42+…+(3n﹣5)*4n﹣2+(3n﹣2)*4n﹣1①,
所以4Tn=1*42+4*43+…+(3n﹣5)*4n﹣1+(3n﹣2)*4n②,
所以①﹣②得:(1﹣4)Tn=1*41+3*42+3*43…+3*4n﹣1﹣(3n﹣2)*4n,
所以﹣3Tn=1*41+3* ![]() ﹣(3n﹣2)*4n,
﹣(3n﹣2)*4n,
所以Tn= ![]() +(n﹣1)4n
+(n﹣1)4n
【解析】(1)由题意得,利用an=Sn﹣Sn﹣1 , 求出数列{an}是等差数列,a1 , a2 , a6是等比数列求出首项为1,即可求出数列{an}的通项;a1 , a2 , a6是等比数列{bn}的前三项求出其公比,即求出{bn}的通项公式;(2)由(1)可知数列{anbn}的通项公式,再由错位相减求和法求出Tn .
【考点精析】掌握等差数列的通项公式(及其变式)和等比数列的通项公式(及其变式)是解答本题的根本,需要知道通项公式:![]() 或
或![]() ;通项公式:
;通项公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4且t≠![]() ;
;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<![]() .
.
其中正确的命题是________(把所有正确命题的序号都填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() 的
的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)∪[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示.
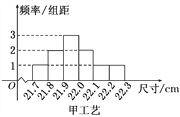
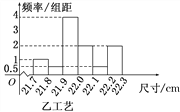
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
附: 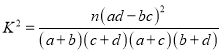
(1)根据上述数据完成下列2×2列联表,根据此数据,你认为选择不同的工艺与生产出一等品是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
(2)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个分类变量X和Y,值域分别为{x1,x2}和{y1,y2},其样本频数分别是a=10,b=21,c+d=35.若X与Y有关系的可信程度不小于97.5%,则c等于( )
A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过圆
过圆![]() 与直线
与直线![]() 的交点,且圆上任意一点关于直线
的交点,且圆上任意一点关于直线![]() 的对称点仍在圆上.
的对称点仍在圆上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且点
两点,且点![]() 是
是![]() 的垂线(垂心是三角形三条高线的交点),求直线
的垂线(垂心是三角形三条高线的交点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列各命题作为原命题,分别写出它们的逆命题、否命题和逆否命题.
(1)若α=β,则sin α=sin β;
(2)若对角线相等,则梯形为等腰梯形;
(3)已知a,b,c,d都是实数,若a=b,c=d,则a+c=b+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ,其中
,其中![]() ,
, ![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com