
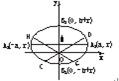
 如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(b>r>0).
如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(b>r>0).| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| r2-b2 |
| 2k1r |
| x1x2 |
| x1+x2 |
| x3x4 |
| x3+x4 |
| r2-b2 |
| 2k1r |
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| x1- p |
| x4-p |
| k2x1 |
| k2x4 |
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| x2 |
| a2 |
| (y-r)2 |
| b2 |
| a2-b2 |
| a2-b2 |
| ||
| a |
| 2k1a2r | ||
b2+a2
|
| a2r2-a2b2 | ||
b2+a2
|
| x1x2 |
| x1+x2 |
| r2-b2 |
| 2k1r |
| x3x4 |
| x3+x4 |
| r2-b2 |
| 2k1r |
| k1x1x2 |
| x1+x2 |
| r2-b2 |
| 2 r |
| k2x3x4 |
| x3+x4 |
| x1- p |
| x4-p |
| k2x1 |
| k2x4 |
| (k1-k2)x1x4 |
| k1x1-k2x4 |
| (k1-k2)x2x3 |
| k1x2-k2x3 |
| k1x1x2 |
| x1+x2 |
| k2x3x4 |
| x3+x4 |
| x2x3 |
| k1x2-k2x3 |
| x3x4 |
| k1x1-k2x4 |
| (k1-k2)x1x4 |
| k1x1-k2x4 |
| (k1-k2)x2x3 |
| k1x2-k2x3 |


科目:高中数学 来源: 题型:
 已知半椭圆
已知半椭圆| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:| c1 |
| a1 |
| c2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•海淀区一模)如图,椭圆
(2006•海淀区一模)如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| FD |
| DP |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,椭圆的中心在原点,长轴AA1在x轴上.以A、A1为焦点的双曲线交椭圆于C、D、D1、C1四点,且|CD|=![]() |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设![]() ,当
,当![]() 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:

(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆的长轴长等于4,Q是椭圆右准线l上异于点A的任意一点,A1、A2分别是椭圆的左、右顶点,直线QA1、QA2与椭圆的另一个交点分别为M、N,求证:直线MN与x轴交于定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com