练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．一次考试中，给出了9道考题，要求考生完成6道题，且前五道题中至少要完成3道，则考生选题解答的选法总数是（　　）
    A．72B．71C．73D．74

    分析 本题需要分类来解，考生从试卷上的9个题目中选6个进行答题，要求至少包含前5个题目中的3个，包含三种情况，即包含3个有C53C43种结果，包含4个有C54C42，包含5个有C55C41，最后相加得到结果．

    解答 解：由题意知，本题需要分类来解，
    考生从试卷上的9个题目中选6个进行答题，
    要求至少包含前5个题目中的3个，包含三种情况，
    即包含3个有C53C43种结果，包含4个有C54C42，包含5个有C55C41，
    根据分类加法得到共有C53C43+C54C42+C55C41=74．
    故选：D．

    点评 本题考查分类计数原理，是一个基础题，分类时要注意观察做完这件事包含几种情况，每种情况包括几种结果，把最后结果相加．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．设实数x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ x≥y\\ 2x-y≤1\end{array}\right.$，则${8^x}•{（\frac{1}{4}）^{-y}}$的最大值是（　　）
    A．64B．32C．2$\sqrt{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数$f（x）=\left\{\begin{array}{l}{log_2}（2-x），0≤x＜k\\{x^3}-3{x^2}+3，k≤x≤a\end{array}\right.$．若存在实数k使得函数f（x）的值域为[-1，1]，则实数a的取值范围是（　　）
    A．$[\frac{3}{2}，1+\sqrt{3}]$B．$[2，1+\sqrt{3}]$C．[1，3]D．[2，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．为了解某市市民的节能意识及行为习惯等情况，某机构在市区范围内进行了一次有关市民节能意识及行为习惯的测试，将所有参加者的笔试成绩（得分均为整数，满分为100分）进行统计，绘制成如下的频数分布表：
     分数（分数段） 频数（人数）
    [60，70） 9
    [70，80） 19
    [80，90） 16
    [90，100] 6
     合计 50
    （1）若采用分层抽样的方法从分数在[60，70）内和[90，100]内的参加者中抽取5人做问卷调查，求这5人中分数在[90，100]内的人数；
    （2）在（1）的条件，从抽取的5人中再随机选取3人进行跟踪调查，记分数在[60，70）内的人数为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知f（x）可导，且$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{2x}$=2，则f′（1）=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=4${\;}^{x-\frac{1}{2}}$+2x+1-1
    （1）判断函数f（x）在定义域上的单调性，并证明；
    （2）若对任意t∈R，不等式f（t2-2t）＞f（k-2t2）恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若x，y∈R，且3x2+2y2=6，则x+y的最大值是$\sqrt{5}$，x2+y2的最小值是2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

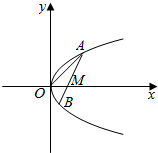    9．如图，线段AB过x轴正半轴上一定点M（m，0），端点A、B到x轴距离之积为2m，以x轴为对称轴，过A，O，B三点作抛物线C．
    （1）求抛物线C的标准方程；
    （2）已知点P（n，2）为抛物线C上的点，过P（n，2）作倾斜角互补的两直线PS，PT，分别交抛物线C于S，T．求证：直线ST的斜率为定值，并求出这个定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

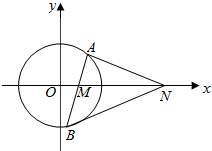    3．已知直线l：4x+3y+10=0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的上方
    （1）求圆C的方程；
    （2）设过点P（1，1）的直线l1被圆C截得的弦长等于2$\sqrt{3}$，求直线l1的方程；
    （3）过点M（1，0）的直线与圆C交于A，B两点（A在x轴上方），问在x轴正半轴上是否存在点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案