
【题目】已知直线l:3x+4y+m=0,圆C:x2+y2-4x+2=0,则圆C的半径r=_____;若在圆C上存在两点A,B,在直线l上存在一点P,使得∠APB=90°,则实数m的取值范围是____.
【答案】![]()
![]()
【解析】
按照直线![]() 与圆
与圆![]() 有无交点分两类讨论,有交点时,显然成立,无交点时,转化为过
有无交点分两类讨论,有交点时,显然成立,无交点时,转化为过![]() 作圆的两条切线的夹角大于等于90°,进一步转化为
作圆的两条切线的夹角大于等于90°,进一步转化为![]() 的最小值小于等于2,转化为圆心
的最小值小于等于2,转化为圆心![]() 到直线的距离小于等于2,据此可得答案.
到直线的距离小于等于2,据此可得答案.
由圆![]() ,得
,得![]() ,所以圆
,所以圆![]() 的半径
的半径![]() .
.
①当直线l:3x+4y+m=0与圆C:x2+y2-4x+2=0有交点时,显然满足题意,
此时![]() ,解得
,解得![]() ,
,
②当直线l:3x+4y+m=0与圆C:x2+y2-4x+2=0无交点时,![]() 或
或![]() ,
,
“在圆C上存在两点A,B,在直线l上存在一点P,使得∠APB=90°”等价于“直线![]() 上存在点
上存在点![]() ,过
,过![]() 作圆的两条切线的夹角大于等于90°”,
作圆的两条切线的夹角大于等于90°”,
设两个切点为![]() 、
、![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
根据题意可得直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,等价于
,等价于![]() ,
,
又![]() 的最小值为圆心
的最小值为圆心![]() 到直线
到直线![]() 的距离,
的距离,
所以![]() ,解得
,解得![]() .又
.又![]() 或
或![]() ,
,
所以![]() 或
或![]() ,
,
由①②可得实数m的取值范围是![]() .
.
故答案为:![]() ;
;![]() .
.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的焦距为2,且过点
(a>b>0)的焦距为2,且过点![]() .
.
(1)求椭圆C的方程;
(2)已知△BMN是椭圆C的内接三角形,若坐标原点O为△BMN的重心,求点O到直线MN距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
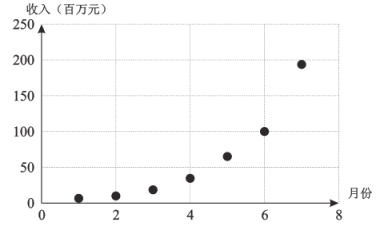
【题目】千百年来,人们一直在通过不同的方式传递信息.在古代,烽火狼烟、飞鸽传书、快马驿站等通信方式被人们广泛传知;第二次工业革命后,科技的进步带动了电讯事业的发展,电报电话的发明让通信领域发生了翻天覆地的变化;之后,计算机和互联网的出现则.使得“千里眼”“顺风耳”变为现实……此时此刻,5G的到来即将给人们的生活带来颠覆性的变革,“5G领先”一方面是源于我国项层设计的宏观布局,另一方面则来自于政府高度重视、企业积极抢滩、企业层面的科技创新能力和先发优势.某科技创新公司基于领先技术的支持,丰富的移动互联网应用等明显优势,随着技术的不断完善,该公司的5G经济收入在短期内逐月攀升,业内预测,该创新公司在第1个月至第7个月的5G经济收入y(单位:百万元)关于月份x的数据如下表:
时间(月份) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
收入(百万元) | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据绘制散点图:
(1)为了更充分运用大数据、人工智能、5G等技术,公司需要派出员工实地考察检测产品性能和使用状况,公司领导要从报名的五名科技人员A、B、C、D、E中随机抽取3个人前往,则A、B同时被抽到的概率为多少?
(2)根据散点图判断,![]() 与
与![]() (a,b,c,d均为大于零的常数)哪一个适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)并根据你判断结果及表中的数据,求出y关于x的回归方程;
(a,b,c,d均为大于零的常数)哪一个适宜作为5G经济收入y关于月份x的回归方程类型?(给出判断即可,不必说明理由)并根据你判断结果及表中的数据,求出y关于x的回归方程;
(3)请你预测该公司8月份的5G经济收入.
参考数据:
|
|
|
|
|
|
462 | 10.78 | 2711 | 50.12 | 2.82 | 3.47 |
其中设![]() ,
,![]()
参考公式:
对于一组具有线性相关系的数据![]() (
(![]() ,2,3,…,n),其回归直线
,2,3,…,n),其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: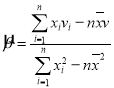 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
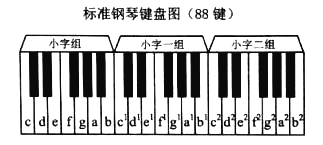
【题目】音乐是用声音来表达人的思想感情的一种艺术,明代的律学家朱载堉创建了十二平均律,并把十二平均律计算得十分精确,与当今的十二平均律完全相同,其方法是将一个八度音程(即相邻的两个具有相同名称的音之间,如图中88键标准钢琴键盘的一部分中,c到c1便是一个八度音程)均分为十二等分的音律,如果用正式的音乐术语称呼原来的7个音符,分别是c,d,e,f,g,a,b,则多出来的5个音符为c#(读做“升c”),d#,f#,g#,a#;12音阶为:c,c#,d,d#,e,f,f#,g,g#,a,a#,b,相邻音阶的频率之比为1:![]() .如图,则键盘c和d的频率之比为
.如图,则键盘c和d的频率之比为![]() 即1:
即1:![]() ,键盘e和f的频率之比为1:
,键盘e和f的频率之比为1:![]() ,键盘c和c1的频率之比为1:2,由此可知,图中的键盘b1和f2的频率之比为( )
,键盘c和c1的频率之比为1:2,由此可知,图中的键盘b1和f2的频率之比为( )
A.![]() B.1:
B.1:![]() C.
C.![]() :1D.
:1D.![]() :1
:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() ,
,![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,![]() 交曲线
交曲线![]() 于另一点
于另一点![]() ,当
,当![]() 变化时,求
变化时,求![]() 的面积的最大值及相应的
的面积的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
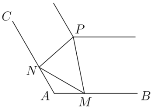
【题目】如图,在郊野公园的景观河的两岸,![]() 、
、![]() 是夹角为120°的两条岸边步道(长度均超过
是夹角为120°的两条岸边步道(长度均超过![]() 千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台
千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台![]() ,在两条步道
,在两条步道![]() 、
、![]() 上分别设立游客上下点
上分别设立游客上下点![]() 、
、![]() ,从
,从![]() 、
、![]() 到观景台
到观景台![]() 建造两条游船观光线路
建造两条游船观光线路![]() 、
、![]() ,测得
,测得![]() 千米.
千米.
(1)求游客上下点![]() 、
、![]() 间的距离;
间的距离;
(2)若![]() ,设
,设![]() ,求两条观光线路
,求两条观光线路![]() 与
与![]() 之和关于
之和关于![]() 的表达式
的表达式![]() ,并求其最大值.
,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
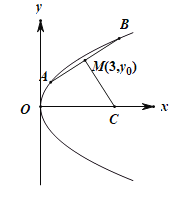
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com