
【题目】田忌赛马是![]() 史记
史记![]() 中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等
中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等![]() 于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注
于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注![]() 假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定:一次比由三场赛马组成,每场由公子和田忌各出一匹马出骞,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
![]() 如果按孙膑的策略比赛一次,求田忌获胜的概率;
如果按孙膑的策略比赛一次,求田忌获胜的概率;
 如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
【答案】(1)0.72;(2)见解析
【解析】
![]() 由题意知,田忌第三场比赛必输,则前两场比赛都胜,因而利用相互独立事件的概率乘法公式可得出答案;
由题意知,田忌第三场比赛必输,则前两场比赛都胜,因而利用相互独立事件的概率乘法公式可得出答案;
![]() 先计算出田忌比赛一次获胜的概率,并计算出田忌比赛一次获利的数学期望,这个期望乘以12即可得出田忌一年赛马获利的数学期望。
先计算出田忌比赛一次获胜的概率,并计算出田忌比赛一次获利的数学期望,这个期望乘以12即可得出田忌一年赛马获利的数学期望。
(1)记事件A:按孙膑的策略比赛一次,田忌获胜,
对于事件A,三场比赛中,由于第三场必输,则前两次比赛中田忌都胜,
因此,![]() ;
;
![]() 设田忌在每次比赛所得奖金为随机变量
设田忌在每次比赛所得奖金为随机变量![]() ,则随机变量
,则随机变量![]() 的可能取值为
的可能取值为![]() 和1000,
和1000,
若比赛一次,田忌获胜,则三场比赛中,田忌输赢的分布为:胜胜胜、负胜胜、胜负胜、胜胜负,
设比赛一次,田忌获胜的概率为![]() ,则
,则![]() .
.
随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
| 1000 |
|
|
|
所以,![]() .
.
因此,田忌一年赛马获利的数学期望为![]() 金。
金。


科目:高中数学 来源: 题型:
【题目】某企业为了增加某种产品的生产能力,决定改造原有生产线,需一次性投资300万元,第一年的年生产能力为300吨,随后以每年40吨的速度逐年递减,根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,该设备的使用年限为3年,该产品的销售利润为1万元![]() 吨.
吨.
![]() 1
1![]() 根据年销售量的频率分布直方图,估算年销量的平均数
根据年销售量的频率分布直方图,估算年销量的平均数![]() 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表![]() ;
;
![]() 2
2![]() 将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
![]() 根据频率分布直方图估计年销售利润不低于180万的概率和不低于220万的概率;
根据频率分布直方图估计年销售利润不低于180万的概率和不低于220万的概率;
![]() 试预测该企业3年的总净利润
试预测该企业3年的总净利润![]() 年的总净利润
年的总净利润![]() 年销售利润一投资费用
年销售利润一投资费用![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
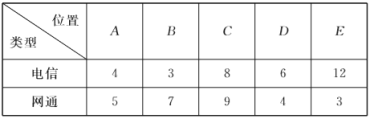
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广.某网游经销商在甲地区![]() 个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
(Ⅰ)如果在测试中掉线次数超过![]() 次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过
次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过![]() 的前提下,能否说明网络状况与网络的类型有关?
的前提下,能否说明网络状况与网络的类型有关?
(Ⅱ)若该游戏经销商要在上述接受测试的电信的![]() 个地区中任选
个地区中任选![]() 个作为游戏推广,求
个作为游戏推广,求![]() 、
、![]() 两地区至少选到一个的概率.
两地区至少选到一个的概率.
参考公式:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
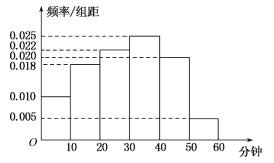
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | 60 | ||
女 | 110 | ||
合计 |
(2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样,抽取8人,再从这8名学生中随机抽取3人参加体育知识问卷调查,记“课外体育不达标”的人数为X,求X的分布列和数学期望.参考公式:![]()
P(K2≥k0) | 0.15 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻的两条对称轴之间的距离为
,其图像相邻的两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列结论正确的是( ).
对称,则下列结论正确的是( ).
A.函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
B.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
C.若![]() ,则
,则![]() 的值为
的值为![]()
D.要得到函数![]() 的图像,只需要将
的图像,只需要将![]() 的图像向右平移
的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 | a | 5 | |
女生 | 40 | d | |
合计 | 100 |
(1)求 a,d 的值,根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取4 位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为 X,求 X 的分布列及数学期望.
附: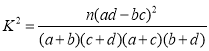
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com