
【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)单调区间;
(3)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.
【答案】
(1)解:因为函数f(x)=ax+x2﹣xlna(a>0,a≠1),
所以f′(x)=axlna+2x﹣lna,f′(0)=0,
又因为f(0)=1,所以函数f(x)在点(0,f(0))处的切线方程为y=1
(2)解:由(1),f′(x)=axlna+2x﹣lna=2x+(ax﹣1)lna.
当a>1时,lna>0,(ax﹣1)lna在R上递增;
当0<a<1时,lna<0,(ax﹣1)lna在R上递增;
故当a>0,a≠1时,总有f′(x)在R上是增函数,
又f′(0)=0,所以不等式f′(x)>0的解集为(0,+∞),
故函数f(x)的单调增区间为(0,+∞),递减区间为 (﹣∞,0)
(3)解:因为存在x1,x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1成立,
而当x∈[﹣1,1]时,|f(x1)﹣f(x2)|≤f(x)max﹣f(x)min,
所以只要f(x)max﹣f(x)min≥e﹣1即可.
又因为x,f'(x),f(x)的变化情况如下表所示:
x | (﹣∞,0) | 0 | (0,+∞) |
f′(x) | ﹣ | 0 | + |
f(x) | 减函数 | 极小值 | 增函数 |
可得f(x)在[﹣1,0]上是减函数,在[0,1]上是增函数,
所以当x∈[﹣1,1]时,f(x)的最小值f(x)min=f(0)=1,
f(x)的最大值f(x)max为f(﹣1)和f(1)中的最大值.
因为 ![]() ,
,
令 ![]() ,因为
,因为 ![]() ,
,
所以 ![]() 在a∈(0,1)、(1,+∞)上是增函数.
在a∈(0,1)、(1,+∞)上是增函数.
而g(1)=0,故当a>1时,g(a)>0,即f(1)>f(﹣1);
当0<a<1时,g(a)<0,即f(1)<f(﹣1).
所以,当a>1时,f(1)﹣f(0)≥e﹣1,即a﹣lna≥e﹣1,
函数y=a﹣lna在a∈(1,+∞)上是增函数,解得a≥e;
当0<a<1时,f(﹣1)﹣f(0)≥e﹣1,即 ![]() ,
,
函数 ![]() 在a∈(0,1)上是减函数,解得
在a∈(0,1)上是减函数,解得 ![]() .
.
综上可知,所求a的取值范围为 ![]()
【解析】(1)先求f′(x),再计算f′(0),和f(0),即可得到切线方程;(2)先求函数的导数f′(x)=axlna+2x﹣lna=2x+(ax﹣1)lna,并且f′(0)=0,判断零点两侧的正负,得到单调区间;(3)将存在性问题转化为|f(x1)﹣f(x2)|max≥e﹣1,即f(x)max﹣f(x)min≥e﹣1,根据上一问的单调性得到最小值f(0),再计算端点值f(﹣1)和f(1)比较大小.因为 ![]() ,再令令
,再令令 ![]() ,求其导数,分情况比较大小,计算a的取值范围.
,求其导数,分情况比较大小,计算a的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() ,
, ![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 方程;
方程;
(Ⅱ)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交
相交![]() 两点,试问在
两点,试问在![]() 轴上是否存在与点
轴上是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商场购物,且参加者必须从淘宝和京东商城选择一家购物.
(1)求这4人中恰有1人去淘宝网购物的概率;
(2)用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数,记X=ξη,求随机变量X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]()
![]() ,且与定直线
,且与定直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹方程为
的轨迹方程为![]() ,直线
,直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)若![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,在
,在![]() 上是否存在点
上是否存在点![]() 使
使![]() 为正三角形?若能,求点
为正三角形?若能,求点![]() 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
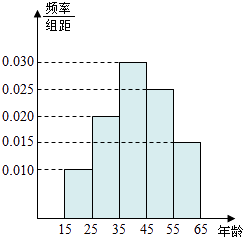
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家生产一种产品,每生产这种产品![]()
![]() (百台),其总成本为
(百台),其总成本为![]() 万元
万元![]() ,其中固定成本为42万元,且每生产1百台的生产成本为15万元
,其中固定成本为42万元,且每生产1百台的生产成本为15万元![]() 总成本
总成本![]() 固定成本
固定成本![]() 生产成本
生产成本![]() 销售收入
销售收入![]() 万元
万元![]() 满足
满足![]() ,假定该产品产销平衡
,假定该产品产销平衡![]() 即生产的产品都能卖掉
即生产的产品都能卖掉![]() ,根据上述条件,完成下列问题:
,根据上述条件,完成下列问题:
![]() 写出总利润函数
写出总利润函数![]() 的解析式
的解析式![]() 利润
利润![]() 销售收入
销售收入![]() 总成本
总成本![]() ;
;
![]() 要使工厂有盈利,求产量
要使工厂有盈利,求产量![]() 的范围;
的范围;
![]() 工厂生产多少台产品时,可使盈利最大?
工厂生产多少台产品时,可使盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com