
【题目】如图,已知圆G:x2﹣x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为 ![]() 的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
(Ⅱ)若焦点F在以线段CD为直径的圆E的外部,求m的取值范围.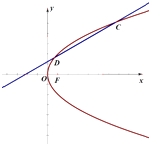
【答案】解:(Ⅰ)∵圆G:x2﹣x+y2=0与x轴交于(0,0),(1,0), 圆G:x2﹣x+y2=0,经过抛物线y2=2px的焦点,
∴抛物线y2=2px的焦点F(1,0),
∴抛物线的方程为:y2=4x.
(Ⅱ)设C(x1 , y1),D(x2 , y2),
∵ ![]() ,则(x1﹣1)(x2﹣1)+y1y2>0,
,则(x1﹣1)(x2﹣1)+y1y2>0,
设l的方程为: ![]() ,
,
于是 ![]()
即 ![]()
由 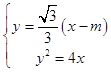 ,得x2﹣(2m+12)x+m2=0,
,得x2﹣(2m+12)x+m2=0,
∴ ![]() ,
,
于是 ![]() ,
,
故 ![]() ,
,
又△=(2m+12)2﹣4m2>0,得到m>﹣3.
∴ ![]() 或m>2
或m>2 ![]() .
.
【解析】(Ⅰ)圆G:x2﹣x+y2=0与x轴交于(0,0),(1,0),从而抛物线y2=2px的焦点F(1,0),由此能求出抛物线的方程.(Ⅱ)设C(x1 , y1),D(x2 , y2),则(x1﹣1)(x2﹣1)+y1y2>0,设l的方程为: ![]() ,则
,则 ![]() ,由
,由 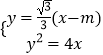 ,得x2﹣(2m+12)x+m2=0,由此利用韦达定理结合已知条件能求出m的取值范围.
,得x2﹣(2m+12)x+m2=0,由此利用韦达定理结合已知条件能求出m的取值范围.


科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE= ![]() ,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为 ![]() .若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为
.若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为 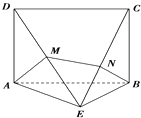
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点. 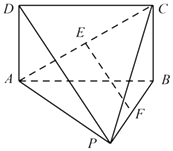
(Ⅰ)求证EF∥平面PCD;
(Ⅱ)求直线DP与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣ ![]() )的定义域为( )
)的定义域为( )
A.[ ![]() ,
, ![]() ]
]
B.[1, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[﹣1, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线![]() .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )
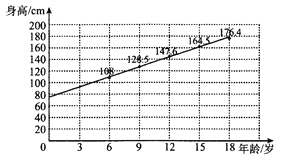
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为![]()
C. 直线![]() 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量
D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+3.
(1)若f(x)在(﹣∞, ![]() ]是减函数,在[
]是减函数,在[ ![]() ,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
(2)求实数a的取值范围,使f(x)在区间[﹣5,5]上是单调函数,并指出相应的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为双曲线C: ![]() =1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( )
=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( ) 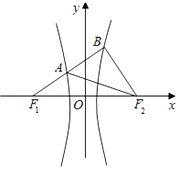
A.(3,+∞)
B.(1,2+ ![]() )
)
C.(3,2+ ![]() )
)
D.(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com