
【题目】设![]() ,函数
,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的零点个数;
的零点个数;
(2)若函数![]() 与函数
与函数![]() 的图象分别位于直线
的图象分别位于直线![]() 的两侧,求
的两侧,求![]() 的取值集合
的取值集合![]() ;
;
(3)对于![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)当n=1时,f(x)=![]() ,f′(x)=
,f′(x)=![]() (x>0),确定函数的单调性,即可求函数y=f(x)的零点个数;
(x>0),确定函数的单调性,即可求函数y=f(x)的零点个数;
(2)若函数y=f(x)与函数y=g(x)的图象分别位于直线y=1的两侧,n∈N*,函数f(x)有最大值f(![]() )=
)=![]() <1,即f(x)在直线l:y=1的上方,可得g(n)=
<1,即f(x)在直线l:y=1的上方,可得g(n)=![]() >1求n的取值集合A;
>1求n的取值集合A;
(3)x1,x2∈(0,+∞),|f(x1)﹣g(x2)|的最小值等价于![]() ,发布网球场相应的函数值,比较大小,即可求|f(x1)﹣g(x2)|的最小值.
,发布网球场相应的函数值,比较大小,即可求|f(x1)﹣g(x2)|的最小值.
(1)当![]() 时,
时,![]() ,
,![]() .
.
由![]() 得
得![]() ;由
;由![]() 得
得![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
因为![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 上存在一个零点;
上存在一个零点;
当![]() 时,
时,![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 上不存在零点.
上不存在零点.
综上得函数![]() 在
在![]() 上存在唯一一个零点.
上存在唯一一个零点.
(2)由函数![]() 求导,得
求导,得![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
则当![]() 时,函数
时,函数![]() 有最大值
有最大值![]() ;
;
由函数![]() 求导,得
求导,得![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() .
.
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
则当![]() 时,函数
时,函数![]() 有最小值
有最小值![]() ;
;
因为![]() ,函数
,函数![]() 的最大值
的最大值![]() ,
,
即函数![]() 在直线
在直线![]() 的下方,
的下方,
故函数![]() 在直线
在直线![]() :
:![]() 的上方,
的上方,
所以![]() ,解得
,解得![]() .
.
所以![]() 的取值集合为
的取值集合为![]() .
.
(3)对![]() ,
,![]() 的最小值等价于
的最小值等价于![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
因为![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称函数
,则称函数![]() 有一个宽为
有一个宽为![]() 的通道.给出下列函数:①
的通道.给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在区间
.其中在区间![]() 上通道宽度为1的函数由__________ (写出所有正确的序号).
上通道宽度为1的函数由__________ (写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
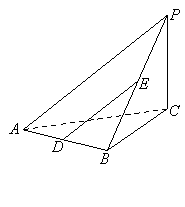
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是边长为2的正方形,且DE=![]() ,平面ABCD⊥平面ADE,∠ADE=30°
,平面ABCD⊥平面ADE,∠ADE=30°

(1)求证:AE⊥平面CDE;
(2)求AB与平面BCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为4 800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(1)求底面积,并用含x的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com