
【题目】如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
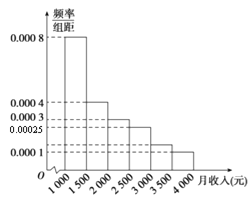
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
【答案】(1)20(2)17750,1962.5
【解析】
(1)先求得月收入在[1000,1500)的频率,即可得到样本容量,求得月收入在[1 500,2 000)的人数,根据分层抽样求得答案;
(2)利用中位数的公式求得中位数,再根据概率和为1求得月收入在[3000,3500)的频率,再利用平均数公式求得结果.
(1)由题知,月收入在[1000,1500)的频率为0.0008×500=0.4,
又月收入在[1000,1500)的有4 000人,故样本容量n![]() 10000.
10000.
又月收入在[1500,2000)的频率为0.000 4×500=0.2,
月收入在[1 500,2 000)的人数为0.2×10000=2 000,
从10 000人中用分层抽样的方法抽出100人,
则月收入在[1500,2000)的这组中应抽取100×![]() =20(人).
=20(人).
(2)月收入在[1000,2000)的频率为0.4+0.2=0.6>0.5,
故样本数据的中位数为1500+![]() =1500+250=1750.
=1500+250=1750.
由频率分布直方图可知, 月收入在[3000,3500)的频率为
![]()
故样本数据的平均数为
![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1-![]() (a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(1)求a的值;
(2)证明:函数f(x)在定义域(-∞,+∞)内是增函数;
(3)当x∈(0,1]时,tf(x)≥2x-2恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取![]() 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取![]() 名学生,并在这
名学生,并在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有![]() 名学生与张老师面谈的概率
名学生与张老师面谈的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i﹣1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1 , l2 , l3 , l4竖直放置在同一水平线上,则大致的图形是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosB=bcosA.
(1)求![]() 的值;
的值;
(2)若sin A=![]() ,求sin(C-
,求sin(C-![]() ) 的值.
) 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com