
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 8 |
| π |
| 12 |
| π |
| 3 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1+cos2z |
| 4 |
| 1 |
| 4 |
| π |
| 6 |
2+
| ||
| 8 |
| 5π |
| 12 |
| π |
| 12 |
2+
| ||
| 8 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2012•江苏二模)选做题
(2012•江苏二模)选做题| PC |
| PA |
| BD |
| DC |
|
| x2 |
| 16 |
| y2 |
| 9 |
| 13 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-3 3.2回归分析练习卷(解析版) 题型:解答题
(本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量
|
x(min) |
l |
2 |
3 |
4 |
5 |
6 |
|
y(mg) |
39.8 |
32.2 |
25.4 |
20.3 |
16.2 |
13.3 |
(1)设x与z之问具有关系 ,试根据测量数据估计c和d的值;
,试根据测量数据估计c和d的值;
(2)估计化学反应进行到10 min时未转化物质的量.
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古巴彦淖尔市高二第一学期期中考试数学 题型:选择题
设x,y满足约束条件 ,若目标函数z =ax + by(a > 0 ,b > 0)的最大值为12 ,则
,若目标函数z =ax + by(a > 0 ,b > 0)的最大值为12 ,则 的最小值为
的最小值为
A . B.
B. 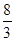 C.
C.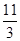 D.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com