
(Ⅰ)求![]() 的通项;
的通项;
(Ⅱ)求![]() 的前n项和
的前n项和![]() 。
。
(21)本小题主要考查等比数列的基本知识,考查分析问题能力和推理能力.
解:(I)由210S30-(210+1)S20+S10=0得
210(S30-S20)=S20-S10,
即 210(a21+a22+…+a30)=a11+a12+…+a20,
可得 210·q10(a11+a12+…+a20)=a11+a12+…+a20.
因为an>0,所以
210q10=1,
解得q=![]() ,因而
,因而
an=a1qn-1=![]() ,n=1,2,….
,n=1,2,….
(II)因为{an}是首项a1=![]() 、公比q=
、公比q=![]() 的等比数列,故
的等比数列,故
Sn= =1-
=1-![]() ,nSn=n-
,nSn=n-![]() .
.
则数列{nSn}的前n项和
Tn=(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() ),
),
![]() (1+2+…+n)-(
(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() ).
).
前两式相减,得
![]() (1+2+…+n)-(
(1+2+…+n)-(![]() +
+![]() +…+
+…+![]() )+
)+![]()
=![]() -
-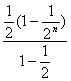 +
+![]() ,
,
即 Tn=![]()


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com