
【题目】选修4-4:坐标系与参数方程
以直角坐标系xOy的原点为极点,x轴的非负半轴为极轴建立极坐标系,且两坐标系相同的长度单位.已知点N的极坐标为( ![]() ,
, ![]() ),M是曲线C1:ρ=1上任意一点,点G满足
),M是曲线C1:ρ=1上任意一点,点G满足 ![]() ,设点G的轨迹为曲线C2 .
,设点G的轨迹为曲线C2 .
(1)求曲线C2的直角坐标方程;
(2)若过点P(2,0)的直线l的参数方程为  (t为参数),且直线l与曲线C2交于A,B两点,求
(t为参数),且直线l与曲线C2交于A,B两点,求 ![]() 的值.
的值.
【答案】
(1)解:由ρ=1,得x2+y2=1,∴曲线C1的直角坐标方程为x2+y2=1,
∵点N的直角坐标为(1,1),设G(x,y),M(x0,y0),又 ![]() ,即(x,y)=(x0,y0)+(1,1),
,即(x,y)=(x0,y0)+(1,1),
∴ ![]() ,代入
,代入 ![]() ,得(x﹣1)2+(y﹣1)2=1,
,得(x﹣1)2+(y﹣1)2=1,
∴曲线C2的直角坐标方程为(x﹣1)2+(y﹣1)2=1
(2)解:把直线l  (t为参数)的方程代入曲线C2的直角坐标方程(x﹣1)2+(y﹣1)2=1,
(t为参数)的方程代入曲线C2的直角坐标方程(x﹣1)2+(y﹣1)2=1,
得 ![]() ,即
,即 ![]() .
.
设A、B两点对应的参数分别为t1、t2,则 ![]() ,易知t1>0,t2>0,
,易知t1>0,t2>0,
∴ ![]()
【解析】(Ⅰ)由ρ=1,得x2+y2=1,可得曲线C1的直角坐标方程为x2+y2=1.设G(x,y),M(x0 , y0),利用向量坐标运算可得点M的坐标用点G的坐标表示,代入曲线C1的方程即可得出方程.(Ⅱ) 把直线l  (t为参数)的方程代入曲线C2的直角坐标方程可得:
(t为参数)的方程代入曲线C2的直角坐标方程可得: ![]() .利用一元二次方程的根与系数的关系即可得出.
.利用一元二次方程的根与系数的关系即可得出.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx,g(x)= ![]() (m>0).
(m>0).
(1)当m=1时,函数y=f(x)与y=g(x)在x=1处的切线互相垂直,求n的值;
(2)若对任意x>0,恒有|f(x)|≥|g(x)|成立,求实数n的值及实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC= ![]() .
. 
(1)求证:BC∥平面AB1C1;
(2)求证:平面A1ABB1⊥平面AB1C1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x)和g(x),如果对任意x∈D,都有|f(x)﹣g(x)|≤1成立,则称f(x)在区间D上可被g(x)替代,D称为“替代区间”.给出以下问题:
①f(x)=x2+1在区间(﹣∞,+∞)上可被g(x)=x2+ ![]() 替代;
替代;
②如果f(x)=lnx在区间[1,e]可被g(x)=x﹣b替代,则﹣2≤b≤2;
③设f(x)=lg(ax2+x)(x∈D1),g(x)=sinx(x∈D1),则存在实数a(a≠0)及区间D1 , D2 , 使得f(x)在区间D1∩D2上被g(x)替代.
其中真命题是( )
A.①②③
B.②③
C.①
D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
(Ⅰ)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(Ⅱ)在线段CD上是否存在一点E,使得直线AE与平面ADM所成角的正弦值为 ![]() ,若存在,请说明点E的位置;若不存在,请说明理由;
,若存在,请说明点E的位置;若不存在,请说明理由;
(Ⅲ)求二面角A﹣MD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若曲线C1是一个圆,且点P(1,1)在圆C1外,求实数m的取值范围;
(2)当m=2时,曲线![]() 关于直线x+1=0对称的曲线为
关于直线x+1=0对称的曲线为![]() ,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线
,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线![]() ,它们分别与曲线C1和曲线
,它们分别与曲线C1和曲线![]() 相交,且直线
相交,且直线![]() 被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,点M在边DC上,点F在边AB上,且
,点M在边DC上,点F在边AB上,且![]() ,垂足为E,若将
,垂足为E,若将![]() 沿AM折起,使点D位于
沿AM折起,使点D位于![]() 位置,连接
位置,连接![]() ,
,![]() 得四棱锥
得四棱锥![]() .
.
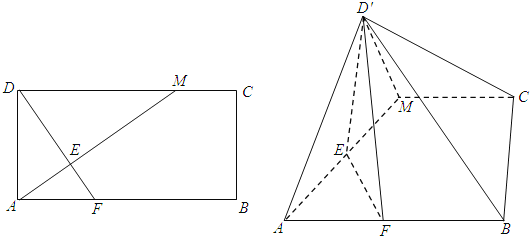
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,直线
,直线![]() 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为![]() ,求直线
,求直线![]() 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
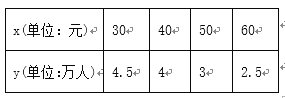
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: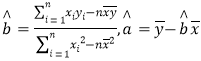
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com