
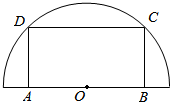
 如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为30cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.分析 (1)连结OC,求出OB,然后求解表达式.
(2)利用基本不等式求出函数的最值即可.
解答  解:(1)连结OC,得$OB=\sqrt{900-{x^2}}$,所以AB=$2\sqrt{900-{x^2}}$,
解:(1)连结OC,得$OB=\sqrt{900-{x^2}}$,所以AB=$2\sqrt{900-{x^2}}$,
所以y=$2x\sqrt{900-{x^2}}$,x∈(0,30)….(8分)
(2)因为$2x\sqrt{900-{x^2}}≤{x^2}+900-{x^2}=900$.
即x2=900-x2,即x=$15\sqrt{2}$时取等号,此时ymax=900…(15分)
答:$BC=15\sqrt{2}$时,矩形ABCD的面积最大,最大为900cm2….(16分)
点评 本题考查函数的解析式的求法,基本不等式的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年份 | 1896年 | 1900年 | 1904年 | … | 2016年 |
| 届数 | 1 | 2 | 3 | … | n |
| A. | 28 | B. | 29 | C. | 30 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5} | B. | {2,4,6} | C. | {2,4} | D. | {1,3,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -9 | C. | -8 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com