
【题目】在![]() 平面上有一点列
平面上有一点列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,对每个正整数
,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]()
![]() 的图像上,且点
的图像上,且点![]() 、点
、点![]() 与点
与点![]() 构成一个以
构成一个以![]() 为顶角顶点的等腰三角形;
为顶角顶点的等腰三角形;
(1)求点![]() 的纵坐标
的纵坐标![]() 的表达式;
的表达式;
(2)若对每个自然数![]() ,以
,以![]() 、
、![]() 、
、![]() 为边长能构成一个三角形,求
为边长能构成一个三角形,求![]() 的取值范围;
的取值范围;
(3)设![]()
![]() ,若
,若![]() 取(2)中确定的范围内的最小整数,问数列
取(2)中确定的范围内的最小整数,问数列![]() 的最大项的项数是多少?试说明理由;
的最大项的项数是多少?试说明理由;
科目:高中数学 来源: 题型:
【题目】如图所示,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,点
,点![]() 处标数字
处标数字![]() ,…以此类推:记格点坐标为
,…以此类推:记格点坐标为![]() 的点(
的点(![]() 均为正整数)处所标的数字为
均为正整数)处所标的数字为![]() ,若
,若![]() ,则
,则![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
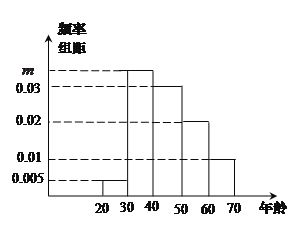
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题
①函数![]() 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
②奇函数的图像一定通过直角坐标系的原点;
③若函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
④设函数![]() 是在区间
是在区间![]() 上图像连续的函数,且
上图像连续的函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]() 上至少有一实根;
上至少有一实根;
其中正确命题的序号是( )
A.(1)B.(2)C.(3)D.(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com