
| A. | (-$\frac{2}{3}\sqrt{21}$,$\frac{2}{3}\sqrt{21}$) | B. | (-2,-1)∪(3,4) | C. | (-$\frac{2}{3}\sqrt{21}$,-1) | D. | ($\frac{2}{3}\sqrt{21}$,4) |
分析 令f(x)=7x2-(k+13)x+k2-k-2,从而可得$\left\{\begin{array}{l}{f(0)={k}^{2}-k-2>0}\\{f(1)=7-k-13+{k}^{2}-k-2<0}\\{f(2)=28-2(k+13)+{k}^{2}-k-2>0}\end{array}\right.$,从而解得.
解答 解:令f(x)=7x2-(k+13)x+k2-k-2,
∵方程7x2-(k+13)x+k2-k-2=0的两根分别在区间(0,1)和(1,2)内,
∴$\left\{\begin{array}{l}{f(0)={k}^{2}-k-2>0}\\{f(1)=7-k-13+{k}^{2}-k-2<0}\\{f(2)=28-2(k+13)+{k}^{2}-k-2>0}\end{array}\right.$,
解得,-2<k<-1或3<k<4;
故选:B.
点评 本题考查了方程的根与函数的零点的关系应用,同时考查了二次不等式的解法.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
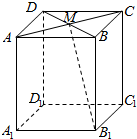 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),
已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com