解:(1)因为f(x)是奇函数,函数的定义域为R,所以f(0)=
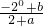
=0,可得b=1,
∴
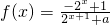
,取f(-1)=-f(1)得
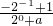
=
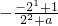
,解之得a=2
因此,
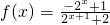
,满足
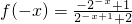
=-

=-f(x),符合题意
所以a=2,b=1
(2)由(1)得,
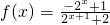
=
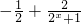
,设x
1<x
2,则
f(x
1)-f(x
2)=
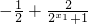
-(
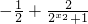
)=
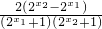
∵y=2
x在实数集上是增函数且函数值恒大于0,
∴

-

>0,

+1>0且

+1>0,可得f(x
1)-f(x
2)>0,即f(x
1)>f(x
2)
∴f(x)在(-∞,+∞)上是单调减函数
(3)∵f(x)是奇函数,
∴f(t
2-2t)+f(2t
2-k)<0,等价于f(t
2-2t)<-f(2t
2-k)=f(k-2t
2),
∵f(x)在(-∞,+∞)上为减函数,
∴由上式可得:t
2-2t>k-2t
2.
即对任意t∈R有:3t
2-2t-k>0,
∴△=4+12k<0?k<-

,即实数k的取值范围是(-∞,-

).
分析:(1)利用特殊值:f(0)=0且f(-1)=-f(1),建立关于a、b的等式并解得a=2,b=1,再将其代入函数表达式加以检验即可;
(2)根据单调性的定义,设x
1<x
2,将f(x
1)与f(x
2)作差,再通分整理,可得这个差是一个正数,从而得到f(x
1)>f(x
2),所以f(x)在(-∞,+∞)上是单调减函数;
(3)根据函数的单调性和奇偶性,将原不等式恒成立转化为关于t的一元二次不等式3t
2-2t-k>0恒成立,再利用一元二次不等式解法结合根的判别式,可求出k的取值范围.
点评:本题给出一个含有指数式的分式形式的函数,叫我们讨论它的单调性与奇偶性,着重考查了函数奇偶性与单调性的综合应用,考查了一元二次不等式恒成立问题等知识,属于中档题.

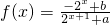 是奇函数.
是奇函数.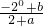 =0,可得b=1,
=0,可得b=1,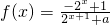 ,取f(-1)=-f(1)得
,取f(-1)=-f(1)得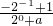 =
=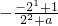 ,解之得a=2
,解之得a=2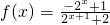 ,满足
,满足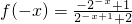 =-
=- =-f(x),符合题意
=-f(x),符合题意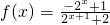 =
=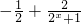 ,设x1<x2,则
,设x1<x2,则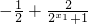 -(
-(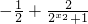 )=
)=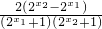
 -
- >0,
>0, +1>0且
+1>0且 +1>0,可得f(x1)-f(x2)>0,即f(x1)>f(x2)
+1>0,可得f(x1)-f(x2)>0,即f(x1)>f(x2) ,即实数k的取值范围是(-∞,-
,即实数k的取值范围是(-∞,- ).
).
