
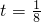 时,计算
时,计算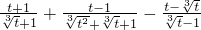 .
.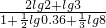 .
.科目:高中数学 来源:2011届上海市普通高等学校高三春季招生数学卷doc 题型:解答题
对于给定首项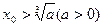 ,由递推公式
,由递推公式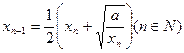 得到数列
得到数列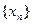 ,对于任意的
,对于任意的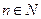 ,都有
,都有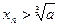 ,用数列
,用数列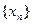 可以计算
可以计算 的近似值。
的近似值。
(1)取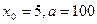 ,计算
,计算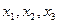 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出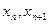 的大小关系;
的大小关系;
(2)当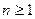 时,证明:
时,证明: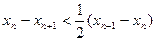 ;
;
(3)当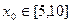 时,用数列
时,用数列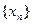 计算
计算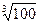 的近似值,要求
的近似值,要求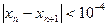 ,请你估计n,并说明理由
,请你估计n,并说明理由
查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高一下学期期中考试数学试卷(解析版) 题型:解答题
已知公差不为0的等差数列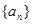 的首项
的首项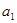 为a
为a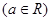 ,设数列的前n项和为
,设数列的前n项和为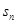 ,且
,且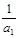 ,
,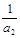 ,
,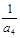 成等比数列.
成等比数列.
(1)求数列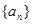 的通项公式及
的通项公式及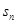 ;
;
(2)记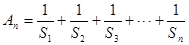 ,
,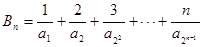 ,当
,当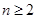 时,计算
时,计算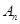 与
与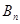 ,并比较
,并比较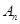 与
与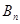 的大小(比较大小只需写出结果,不用证明).
的大小(比较大小只需写出结果,不用证明).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市普通高等学校高三春季招生数学卷 题型:解答题
对于给定首项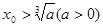 ,由递推公式
,由递推公式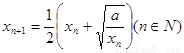 得到数列
得到数列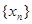 ,对于任意的
,对于任意的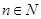 ,都有
,都有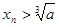 ,用数列
,用数列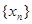 可以计算
可以计算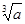 的近似值。
的近似值。
(1)取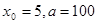 ,计算
,计算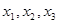 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出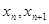 的大小关系;
的大小关系;
(2)当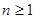 时,证明:
时,证明: ;
;
(3)当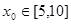 时,用数列
时,用数列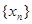 计算
计算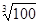 的近似值,要求
的近似值,要求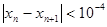 ,请你估计n,并说明理由
,请你估计n,并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
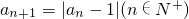 .
.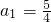 ,计算a2,a3,a4的值,并写出数列{an}(n∈N+,n≥2)的通项公式;
,计算a2,a3,a4的值,并写出数列{an}(n∈N+,n≥2)的通项公式;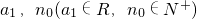 ,使得当
,使得当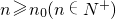 时,an恒为常数,若存在,求出a1,n0,否则说明理由;
时,an恒为常数,若存在,求出a1,n0,否则说明理由;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com