
【题目】已知关于x的不等式组
(1) 若k=1,求不等式组的解集;
(2) 若不等式组的整数解的集合为{-2},求实数k的取值范围.
【答案】(1){x|-![]() <x<-1};(2)-3≤k<2.
<x<-1};(2)-3≤k<2.
【解析】试题分析:(1)将k=1代入求解两个方程求交集即可.
(2)根据-2是方程的根,代入求得k的范围,再求出另一根,根据范围求解即可.
试题解析:
(1) 当k=1时,由2x2+7x+5<0,得-![]() <x<-1;
<x<-1;
由x2-x-2>0,解得x<-1或x>2.
∴ 当k=1时,不等式组的解集是{x|-![]() <x<-1}.
<x<-1}.
(2) ∵ 不等式组的整数解的集合为{-2},
∴ -2是2x2+(2k+5)x+5k<0的解,
∴ k<2,-k>-![]() .
.
又方程2x2+(2k+5)x+5k=0的两根为-k与-![]() ,
,
∴ 2x2+(2k+5)x+5k<0的解是-![]() <x<-k.
<x<-k.
由于不等式组的整数解的集合为{-2},
∴ -2<-k≤3,解得-3≤k<2,即k的取值范围是-3≤k<2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若![]() <t<
<t<![]() ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及![]() 内各有一个实数根.
内各有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|-5<x<5},B={x|0≤x<7},求:(1)A∩B;(2)A∪B;(3)A∪(UB);(4)B∩(UA);(5)(UA)∩(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过5吨时,每吨为![]() 元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费
元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费![]() 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为![]() 吨。
吨。
(1)求![]() 关于
关于![]() 的函数。
的函数。
(2)若甲、乙两户该月共交水费![]() 元,分别求甲、乙两户该月的用水量和水费。
元,分别求甲、乙两户该月的用水量和水费。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 是奇函数,函数
是奇函数,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() 上单调递减,根据单调性的定义求实数
上单调递减,根据单调性的定义求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在区间
在区间![]() 上有且仅有两个不同的零点,求实数
上有且仅有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a﹣![]() (a∈R)
(a∈R)
(Ⅰ)判断函数f(x)在R上的单调性,并用单调函数的定义证明;
(Ⅱ)是否存在实数a使函数f(x)为奇函数?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=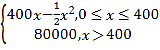 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)已知不等式![]()
![]() 恒成立,若方程
恒成立,若方程![]() 恰有两个不等实根,求
恰有两个不等实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com