练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】由于疫情影响，今年我们学校开展线上教学，高一年级某班班主任为了了解学生上网学习时间，对本班40名学生某天上网学习时间进行了调查，将数据（取整数）整理后，绘制出如图所示频率分布直方图，已知从左到右各个小组的频率分别是0.15，0.25，0.35，0.20，0.05，则根据直方图所提供的信息.

    （1）这一天上网学习时间在分钟之间的学生有多少人？

    （2）这40位同学的线上平均学习时间是多少？

    （3）如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间，这样推断是否合理？为什么？

    【答案】（1）14人（2）104.9分钟（3）这样推断不合理.见解析

    【解析】

    （1）根据频数样本容量频率计算即可；

    （2）根据每组的中值与频率积的和即可估计总体的平均值；

    （3）根据样本的构成来分析，不够全面，所以推断不合理.

    （1）因为频数样本容量频率，一天上网学习时间在分钟之间的学生所占频率为0.35,

    所以一天上网学习时间在分钟之间的学生人数为（人）

    （2）40位同学的线上学习时间为：

    分钟

    （3）因为该样本的选取只在高一某班，不具有代表性，所以这样推断不合理.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，椭圆的方程为(为参数)；以原点为极点，以轴正半轴为极轴建立极坐标系，圆的极坐标方程为．

    （1）求椭圆的极坐标方程，及圆的直角坐标方程；

    （2）若动点在椭圆上，动点在圆上，求的最大值；

    （3）若射线分别与椭圆交于点，求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的极坐标方程为，直线：，直线：.以极点为原点，极轴为轴的正半轴建立平面直角坐标系.

    （1）求直线，的直角坐标方程以及曲线的参数方程；

    （2）已知直线与曲线交于，两点，直线与曲线交于，两点，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设z1是虚数，z2＝z1是实数，且﹣1≤z2≤1．

    （1）求|z1|的值以及z1的实部的取值范围；

    （2）若ω，求证ω为纯虚数；

    （3）求z2﹣ω2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间；

    （2）若恒成立，试确定实数的取值范围；

    （3）证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

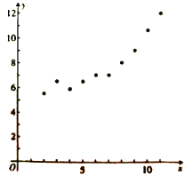
    【题目】某公司近年来特别注重创新产品的研发，为了研究年研发经费(单位：万元)对年创新产品销售额(单位：十万元)的影响，对近10年的研发经费与年创新产品销售额（其中）的数据作了初步处理，得到如图的散点图及一些统计量的值.

    其中，，，，

    .现拟定关于的回归方程为.

    （1）求，的值(结果精确到)；

    （2）根据拟定的回归方程,预测当研发经费为万元时,年创新产品销售额是多少？

    参考公式：

    求线性回归方程系数公式 ：，.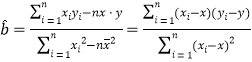

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是边长为2的正方形，平面 为等腰直角三角形，,为的中点，为的中点.

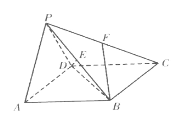
    (1)求异面直线与所成角的余弦值；

    (2)求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知， 是椭圆的左右焦点， 为椭圆的上顶点，点在椭圆上，直线与轴的交点为， 为坐标原点，且， ．

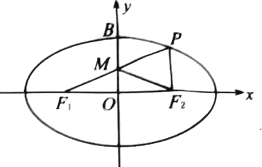
    （1）求椭圆的方程；

    （2）过点作两条互相垂直的直线分别与椭圆交于， 两点（异于点），证明：直线过定点，并求该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    (1)解关于的不等式；

    (2)若不等式的解集为，求实数的值．

    查看答案和解析>>

    同步练习册答案