
【题目】已知函数![]() 在
在![]() 上没有最小值,则
上没有最小值,则![]() 的取值范围是________________.
的取值范围是________________.
【答案】![]()
【解析】
先求导,利用f′(x)=0时,x=0或x=![]() ,讨论两个极值点与(-1,1)的关系,再根据导数和函数的单调性最值的关系将极值与端点处函数值作比较得到a的范围.
,讨论两个极值点与(-1,1)的关系,再根据导数和函数的单调性最值的关系将极值与端点处函数值作比较得到a的范围.
∵f(x)=x3﹣ax,∴f′(x)=3x2﹣2ax=x(3x-2a),当f′(x)=0时,x=0或x=![]() ,
,
(1)当![]() ∈(﹣∞,﹣1]时,即a
∈(﹣∞,﹣1]时,即a![]() 时,f(x)在(-1,0)单调递减,在(0,1)单调递增,此时x=0时f(x)取得最小值,所以舍去.
时,f(x)在(-1,0)单调递减,在(0,1)单调递增,此时x=0时f(x)取得最小值,所以舍去.
(2)当-1<![]() <0时,f(x)在(-1,
<0时,f(x)在(-1,![]() )单调递增,在(
)单调递增,在(![]() ,0)单调递增减,在(0,1)单调递增,由题意
,0)单调递增减,在(0,1)单调递增,由题意![]() 在
在![]() 上没有最小值,
上没有最小值,
则有
(3)当a=0时,f(x)=![]() 在
在![]() 上显然没有最小值,故成立.
上显然没有最小值,故成立.
(4)当0<![]() <1时,f(x)在(-1,
<1时,f(x)在(-1,![]() )单调递增,在(0,
)单调递增,在(0,![]() )单调递增减,在(
)单调递增减,在(![]() ,1)单调递增,由题意
,1)单调递增,由题意![]() 在
在![]() 上没有最小值,
上没有最小值,
则有
(5)当![]() 时,即a
时,即a![]() 时,f(x)在(-1,0)单调递增,在(0,1)单调递减,
时,f(x)在(-1,0)单调递增,在(0,1)单调递减,
此时f(x)在![]() 上没有最小值.
上没有最小值.
综上:a>-1.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,AD=DC=AP=2,AB=1,点E为棱PC的中点.
,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下表:
1,2,3,
4,5,6,7,8,
9,10,11,12,13,14,15,
16,17,18,19,20,21,22,23,24,
……
问:(1)此表第![]() 行的第一个数与最后一个数分别是多少?
行的第一个数与最后一个数分别是多少?
(2)此表第![]() 行的各个数之和是多少?
行的各个数之和是多少?
(3)2019是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,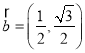 ,函数
,函数![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的实数根
上有两个不同的实数根![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若直线![]() 过点
过点![]() 且被圆
且被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的方程;
的方程;
(2)从圆![]() 外一点
外一点![]() 向圆
向圆![]() 引一条切线,切点为
引一条切线,切点为![]() 为坐标原点,满足
为坐标原点,满足![]() ,求点
,求点![]() 的轨迹方程及
的轨迹方程及![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,延长
,延长![]() 交双曲线右支于点
交双曲线右支于点![]() .若线段
.若线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,则
为坐标原点,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]()
C. ![]() D. 无法确定
D. 无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引中学生去某基地参加夏令营,推出如下收费标准:若夏令营人数不超过30,则每位同学需交费用600元;若夏令营人数超过30,则营员每多1人,每人交费额减少10元(即:营员31人时,每人交费590元,营员32人时,每人交费580元,以此类推),直到达到满额70人为止.
(1)写出夏令营每位同学需交费用![]() (单位:元)与夏令营人数
(单位:元)与夏令营人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当夏令营人数为多少时,旅行社可以获得最大收入?最大收入是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com