【答案】
分析:(I)求导函数,对参数a进行讨论,利用导数的正负,确定函数的单调区间;
(II)确定f(x)的极大值为f(0)=a+b,f(x)的极小值为f(a)=a+b-a
3,要使f(x)有三个不同的零点,则

,从而得证;
(III)先确定|x
1-x
2|=

,并求得其最小值,假设存在实数m满足条件,则m
2+tm+1≤(

)
min,即m
2+tm+1≤4,即m
2+tm-3≤0在t∈[-1,1]上恒成立,从而可求m的范围.
解答:(I)解:∵f′(x)=6x
2-6ax=6x(x-a),
当a=0时,f′(x)=6x≥0,于是f(x)在R上单调递增;
当a>0时,x∈(0,a),f′(x)<0,得f(x)在(0,a)上单调递减;
x∈(-∞,0)∪(a,+∞),f′(x)>0,得f(x)在(-∞,0),(a,+∞)上单调递增;
当a<0时,x∈(a,0),f′(x)<0,得f(x)在(0,a)上单调递减;
x∈(-∞,a)∪(0,+∞),f′(x)>0,得f(x)在(-∞,a),(0,+∞)上单调递增.
综上所述:当a=0时,f(x)的增区间为(-∞,+∞);
当a>0时,f(x)的增区间为(-∞,0),(a,+∞),f(x)的减区间为(0,a);
当a<0时,f(x)的增区间为(-∞,a),(0,+∞),f(x)的减区间为(a,0).…(3分)
(II)证明:当a>0时,由(I)得f(x)在(-∞,0),(a,+∞)上是增函数,f(x)在(0,a)上是减函数;
则f(x)的极大值为f(0)=a+b,f(x)的极小值为f(a)=a+b-a
3.
要使f(x)有三个不同的零点,则

,即
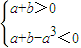
可得-a<b<a
3-a.…(8分)
(III)解:由2x
3-3ax
2+a+b=x
3-2ax
2+3x+a+b,得x
3-ax
2-3x=0即x(x
2-ax-3)=0,
由题意得x
2-ax-3=0有两非零实数根x
1,x
2,则x
1+x
2=a,x
1x
2=-3,
∴|x
1-x
2|=

.
∵f (x)在[1,2]上是减函数,
∴f′(x)=6x
2-6ax=6x(x-a)≤0在[1,2]上恒成立,其中x-a≤0即x≤a在[1,2]上恒成立,
∴a≥2.
∴

≥4.
假设存在实数m满足条件,则m
2+tm+1≤(

)
min,即m
2+tm+1≤4,即m
2+tm-3≤0在t∈[-1,1]上恒成立,
∴

,解得

≤m≤

.
∴存在实数m满足条件,此时m∈[

,

]. …(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查函数的极值与最值,考查恒成立问题,综合性强.

 ,从而得证;
,从而得证; ,并求得其最小值,假设存在实数m满足条件,则m2+tm+1≤(
,并求得其最小值,假设存在实数m满足条件,则m2+tm+1≤( )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,从而可求m的范围.
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,从而可求m的范围. ,即
,即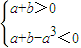
 .
. ≥4.
≥4. )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立, ,解得
,解得 ≤m≤
≤m≤ .
. ,
, ]. …(14分)
]. …(14分)
