
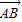 绕其起点沿逆时针方向旋转θ角,得到向量
绕其起点沿逆时针方向旋转θ角,得到向量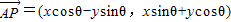 ,叫做把点B绕点A逆时针方向旋转θ角得到点P
,叫做把点B绕点A逆时针方向旋转θ角得到点P ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转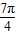 后得到点P,求点P的坐标
后得到点P,求点P的坐标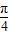 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程. ,
,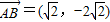 ,根据把点B绕点A沿逆时针方向旋转
,根据把点B绕点A沿逆时针方向旋转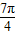 后得到点P,
后得到点P,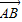 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到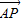 ,由此可得
,由此可得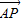 的坐标,从而可求点P的坐标
的坐标,从而可求点P的坐标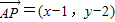 ,
,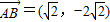 …(2分)
…(2分)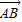 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到 ,
,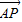 =
=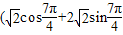 ,
,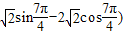 =(-1,-3)…(6分)
=(-1,-3)…(6分)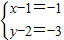 ,解得x=0,y=-1 …(7分)
,解得x=0,y=-1 …(7分)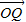 绕O逆时针方向旋转
绕O逆时针方向旋转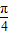 后得到的点Q′(x′,y′),则
后得到的点Q′(x′,y′),则 …(10分)
…(10分)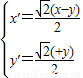 …(11分)
…(11分)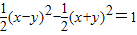 …(13分)
…(13分) …(14分)
…(14分)

科目:高中数学 来源: 题型:
| AB |
| AP |
| 2 |
| 2 |
| 7π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:广东省普宁二中2011-2012学年高二11月月考数学理科试题 题型:044
已知对任意的平面向量,把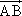 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转![]() 角,得到向量
角,得到向量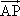 =(xcos
=(xcos![]() -ysin
-ysin![]() ,xsin
,xsin![]() +ycos
+ycos![]() ),叫做把点B绕点A逆时针方向旋转
),叫做把点B绕点A逆时针方向旋转![]() 角得到点P
角得到点P
①已知平面内的点A(1,2),B![]() ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转![]() 后得到点P,求点P的坐标
后得到点P,求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转![]() 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年度广东省普宁第二中学高二上学期11月月考理科数学试卷 题型:解答题
(本题满分12分)已知对任意的平面向量,把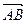 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转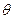 角,得到向量
角,得到向量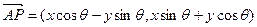 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转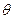 角得到点P
角得到点P
①已知平面内的点A(1,2),B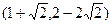 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转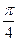 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线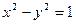 ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2013届度广东省高二上学期11月月考理科数学试卷 题型:解答题
(本题满分12分)已知对任意的平面向量,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角,得到向量
角,得到向量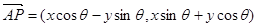 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 角得到点P
角得到点P
①已知平面内的点A(1,2),B ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线 ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com