练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，直线l的参数方程为 （t为参数），若以O为极点，x轴的正半轴为极轴且取相同的单位长度建立极坐标系，曲线C的极坐标方程为.

    （1）求曲线C的直角坐标方程及直线l的普通方程；

    （2）将所得曲线C向右平移1个单位长度，再将曲线C上的所有点的横坐标变为原来的2倍，得到曲线，求曲线上的点到直线l的距离的最大值.

    【答案】（1），；（2）

    【解析】

    （1）根据参数方程与普通方程互化法则，消参即可得到普通方程，根据即可将极坐标方程化为直角坐标方程；

    （2）根据平移法则得出的方程，将问题转化为求圆上的点到直线距离的最大值.

    （1）由得，即

    故直线l的普通方程为；

    将代入得，即.

    故曲线C的直角坐标方程为

    （2）将所得曲线C向右平移1个单位长度，得

    再将曲线C上的所有点的横坐标变为原来的2倍，得.即

    因为曲线的圆心为，半径为

    且圆心到直线的距离为

    所以曲线上的点到直线l的距离的最大值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线与直线互相垂直，且交点为Q，点，线段QF的垂直平分线与直线交于点P．

    （I）若动点P的轨迹为曲线E，求曲线E的方程；

    （Ⅱ）已知点，经过点M的两条直线分别与曲线E交于A，B和C，D，且，设直线AC，BD的斜率分别为，是否存在常数，使得当变动时，？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝log3（ax+b）的图象经过点A（2，1）和B（5，2），an＝an+b（n∈N*）．

    （1）求{an}；

    （2）设数列{an}的前n项和为Sn，bn，求{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，，过点作平面的垂线，垂足为与的交点，是线段的中点.

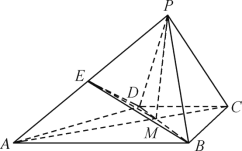
    （1）求证：DE//平面；

    （2）若四棱锥的体积为，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着城市化、工业化进程加速，汽车工业快速发展，国际原油供求矛盾逐步加深，全球气候变暖日益明显.在此背景下，以节能减排为重要目标的新能源汽车技术不断取得突破，并呈现快速突破、竞相发展的态势.在2015年10月份，国家发改委等部委在《电动汽车充电基础设施发展指南（2015-2020年）》中要求，新建住宅配建停车位应100%建设充电基础设施或预留建设安装条件，大型公共建筑物配建停车场、社会公共停车场建设充电基础设施或预留建设安装条件的车位比例不低于10%，每2000辆电动汽车应至少配套建设一座公共充电站.

    为鼓励新能源汽车发展，国家和地方出台了相关补贴政策.

    附表1：2018年某市新能源汽车补贴政策：

    纯电续航里程（）

    国家补贴（万元/辆）

    地方补贴（万元/辆）

    1.50

    0.75

    2.4

    1.2

    3.4

    1.7

    4.5

    2.25

    5

    2.5

    为了获得更大的市场分额，抢占未来新能源汽车销售先机.该市对2018年各类型新能源汽车销售占比情况进行了调查.

    附表2：2018年该市各类型新能源汽车销售占比情况：

    纯电续航里程

    占比

    5%

    20%

    35%

    25%

    15%

    （1）用2018年新能源汽车销售占比来估计2019年的新能源汽车销售情况，求2019年每辆新能源汽车的平均补贴.若该市2019年想实现3000万元补贴，估计需要销售新能源汽车多少量.（补贴政策按每辆车补贴=国家补贴+地方补贴，结果四舍五入保留整数）

    （2）该市新能源汽车促进办公宝为了调查新能源汽车补贴发放情况，希望从2018年销售的新能漂源汽车中抽取10辆车的信息进行回访核实.以各类型新能源汽车销售占比为概率.求抽到几辆续航里程小于新能源汽车的可能性最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对数列，规定为数列的一阶差分数列，其中，规定为的二阶差分数列，其中.

    （1）数列的通项公式，试判断，是否为等差数列，请说明理由？

    （2）数列是公比为的正项等比数列，且，对于任意的，都存在，使得，求所有可能的取值构成的集合；

    （3）各项均为正数的数列的前项和为，且，对满足，的任意正整数、、，都有，且不等式恒成立，求实数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知有穷数列A：（且）.定义数列A的“伴生数列”B：，其中（），规定，.

    （1）写出下列数列的“伴生数列”：

    ①1，2，3，4，5；

    ②1，，1，，1.

    （2）已知数列B的“伴生数列”C：，，…，，…，，且满足（，2，…，n）.

    （i）若数列B中存在相邻两项为1，求证：数列B中的每一项均为1；

    （ⅱ）求数列C所有项的和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,矩形中,,,为的中点,点,分别在线段,上运动（其中不与,重合,不与,重合）,且,沿将折起,得到三棱锥,则三棱锥体积的最大值为__________；当三棱锥体积最大时,其外接球的表面积的值为_______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列（）的各项均为正整数，且.若对任意，存在正整数使得，则称数列具有性质.

    （1）判断数列与数列是否具有性质；（只需写出结论）

    （2）若数列具有性质，且，，，求的最小值；

    （3）若集合，且（任意，）.求证：存在，使得从中可以选取若干元素（可重复选取）组成一个具有性质的数列.

    查看答案和解析>>

    同步练习册答案