
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2![]() ;
;
(2)当b>1时,证明对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() ;?
;?
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.?
(1)证明:依题意知,对任意x∈R,都有f(x)≤1.
∵f(x)=-b(x-![]() )2+
)2+![]() ,
,
∴f(![]() )=
)=![]() ≤1.
≤1.
∵a>0,b>0,∴a≤2b.?
(2)证明:必要性:对任意x∈[0,1],|f(x)|≤1![]() f(x)≥-1,?
f(x)≥-1,?
∴f(1)≥-1,即a-b≥-1.∴a≥b-1.?
对任意x∈[0,1],|f(x)|≤1![]() f(x)≤1,?
f(x)≤1,?
∵b>1,可以推出f(![]() )≤1,
)≤1,
即a·![]() -1≤1,
-1≤1,
∴a≤2![]() .∴b-1≤a≤2
.∴b-1≤a≤2![]() .?
.?
充分性:∵b>1,a≥b-1,对任意x∈[0,1],可以推出ax-bx2≥b(x-x2)-x≥-x≥-1,即ax-bx2≥-1.
∵b>1,a≤2![]() .对任意x∈[0,1],可以推出ax-bx2≤2bx-bx2≤1,即ax-bx2≤1.
.对任意x∈[0,1],可以推出ax-bx2≤2bx-bx2≤1,即ax-bx2≤1.
∴-1≤f(x)≤1.?
综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() .
.
(3)解:∵a>0,0<b≤1时,对任意x∈[0,1],有f(x)=ax-bx2≥-b≥-1,即f(x)≥-1.
f(x)≤1![]() f(1)≤1
f(1)≤1![]() a-b≤1,即a≤1+b.
a-b≤1,即a≤1+b.
a≤1+b![]() f(x)≤(1+b)x-bx2≤1,即f(x)≤1.
f(x)≤(1+b)x-bx2≤1,即f(x)≤1.
∴当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤1+b.?
温馨提示:本题主要考查二次函数、不等式、充要条件的综合应用,考查分类讨论思想和逻辑推理能力以及思维能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤![]() ;
;
(2)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆(x+1)2+y2=1相切,求a的值;?
(2)求函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练15练习卷(解析版) 题型:选择题
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
(A)?x∈R,f(x)≤f(x0) (B)?x∈R,f(x)≥f(x0)
(C)?x∈R,f(x)≤f(x0) (D)?x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高二下学期第二次月考数学文卷 题型:选择题
已知a>0,函数f(x)= 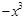 +ax在[1,+∞)上是减函数,则a的取值范围是(
)
+ax在[1,+∞)上是减函数,则a的取值范围是(
)
A. a≥1 B. 0<a≤2 C. 0<a≤3 D. 1≤a≤3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com