
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6, 0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买k台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.
(1)0.31 (2)3
解析试题分析:(1)至少3人需使用设备分为恰好有3人使用的设备和4个人使用设备.这两个是事件是互斥事件,首先利用独立事件的概率公式分别求出恰好有3人使用的设备和4个人使用设备的概率,最后相加即可.
利用独立事件的概率公式和互斥事件的概率公式计算出同一工作日4人需使用设备的概率.然后结合(1)的结论即可得出结论.
试题解析:记Ai表示事件:同一工作日乙、丙中恰有i人需使用设备,i=0,1,2.
B表示事件:甲需使用设备.
C表示事件:丁需使用设备.
D表示事件:同一工作日至少3人需使用设备.
E表示事件:同一工作日4人需使用设备.
F表示事件:同一工作日需使用设备的人数大于k.
(1)D=A1·B·C+A2·B+A2·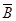 ·C
·C
P(B)=0.6,P(C)=0.4,P(Ai)=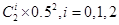 .
.
所以P(D)=P(A1·B·C+A2·B+A2·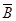 ·C)= P(A1·B·C)+P(A2·B)+P(A2·
·C)= P(A1·B·C)+P(A2·B)+P(A2·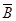 ·C)
·C)
= P(A1P)·P(B)·P(C)+P(A2)·P(B)+P(A2)·p(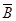 )·p(C)=0.31.
)·p(C)=0.31.
(2)由(1)知,若k=3,则P(F)==0.31>0.1.
又E=B·C·A2,P(E)=P(B·C·A2)= P(B)·P(C)·P(A2)=0.06;
若k=4,则P(F)=0.06<0.1.
所以k的最小值为3.
考点:1.独立事件的概率;2.互斥事件的概率.


科目:高中数学 来源: 题型:解答题
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
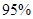 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?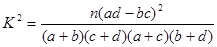 ,其中
,其中 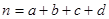
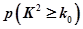 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为ξ,求ξ的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
| | 不得禽流感 | 得禽流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(1)从中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下: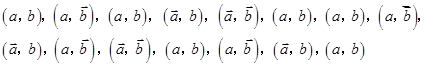
其中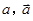 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;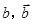 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
(1)若某组成功研发一种新产品,则给改组记1分,否记0分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(2)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
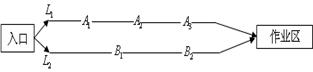
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有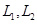 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图),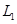 巷道有
巷道有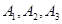 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是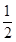 ;
;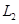 巷道有
巷道有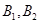 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为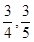 .
.
(1)求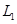 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若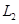 巷道中堵塞点个数为
巷道中堵塞点个数为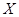 ,求
,求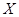 的分布列及数学期望
的分布列及数学期望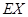 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定是去打球、唱歌还是去下棋。游戏规则为:以O为起点,再从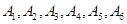 (如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为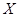 ,若
,若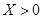 就去打球,若
就去打球,若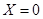 就去唱歌,若
就去唱歌,若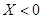 就去下棋。
就去下棋。
(1)写出数量积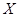 的所有可能值;
的所有可能值;
(2)分别求小波去下棋的概率和不去唱歌的概率。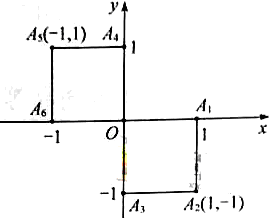
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com