
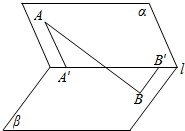
 如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.
如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.分析 (1)在平面α内,过B′作B′C∥A′A,过A作AC∥A′B′,交B′C于点C,则四边形AA′B′C是矩形,由余弦定理得求出BC,由此能求出AB.
(2)由AC∥l,得∠BAC是AB与l所成的角,由此能求出AB与l所成的角的大小.
解答 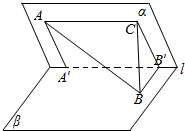 解:(1)在平面α内,过B′作B′C∥A′A,过A作AC∥A′B′,交B′C于点C,
解:(1)在平面α内,过B′作B′C∥A′A,过A作AC∥A′B′,交B′C于点C,
∵二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,
BB′⊥l交1于B′,AA′=2,BB′=1,A′B′=$\sqrt{3}$,
∴四边形AA′B′C是矩形,AC=A′B′=$\sqrt{3}$,B′C=AA′=2,∠BB′C=60°,
∴BC=$\sqrt{B{{B}^{'}}^{2}+{B}^{'}{C}^{2}-2×B{B}^{'}×{B}^{'}C×cos60°}$=$\sqrt{1+4-2×1×2×\frac{1}{2}}$=$\sqrt{3}$,
∵l⊥BB′,l⊥B′C,AC∥l,
∴AC⊥平面BB′C,∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{3+3}$=$\sqrt{6}$.
(2)∵AC∥l,∴∠BAC是AB与l所成的角,
∵$AC=BC=\sqrt{3}$,AC⊥BC,
∴∠BAC=45°,
∴AB与l所成的角为45°.
点评 本题考查两直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
 如图所示的封闭区域的边界是由两个关于x轴对称的半圆与截取于同一双曲线的两段曲线组合而成的,其中上半圆所在圆的方程是x2+y2-4y-4=0,双曲线的左右顶点A、B是该圆与x轴的交点,双曲线与该圆的另两个交点是该圆平行于x轴的一条直径的两个端点.
如图所示的封闭区域的边界是由两个关于x轴对称的半圆与截取于同一双曲线的两段曲线组合而成的,其中上半圆所在圆的方程是x2+y2-4y-4=0,双曲线的左右顶点A、B是该圆与x轴的交点,双曲线与该圆的另两个交点是该圆平行于x轴的一条直径的两个端点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com