练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知直线m，n和平面α，如果n?α，那么“m⊥n”是“m⊥α”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充分必要条件D．既不充分也不必要条件

    分析 根据线面垂直的判定定理以及充分条件和必要条件的定义进行判断即可．

    解答 解：若m⊥α，则m⊥n，即必要性成立，
    当m⊥n时，m⊥α不一定成立，必须m垂直平面α内的两条相交直线，即充分性不成立，
    故“m⊥n”是“m⊥α”的必要不充分条件，
    故选：B

    点评 本题主要考查充分条件和必要条件的判断，结合线面垂直的判定定理是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．设α，β是两个不同的平面，l，m是两条不同的直线，且l?α，m?β下面命题正确的是（　　）
    A．若l∥β，则α∥βB．若α⊥β，则l⊥mC．若l⊥β，则α⊥βD．若α∥β，则l∥m

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律．对捕食者和被捕食者数量之间的关系描述正确的是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知正方形ABCD边长为2，E为AB边上一点，则$\overrightarrow{ED}$•$\overrightarrow{EC}$的最小值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

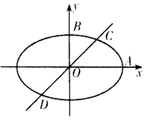    17．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{3}}{2}$，且过点（$\frac{\sqrt{3}}{2}$，$\frac{1}{4}$）．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）已知A、B分别为椭圆E的右顶点、上顶点，过原点O做斜率为k（k＞0）的直线交椭圆于C、D两点，求四边形ACBD面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若x，y满足$\left\{\begin{array}{l}{x+y-2≤0}\\{2x+y-2≥0}\\{y≥0}\end{array}\right.$，则z=2x-y的最大值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知$\frac{sinα+cosα}{sinα-cosα}$=2，则sin2α-sinαcosα的值为$\frac{3}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=lnx-a（x-1），g（x）=ex，其中e为自然对数的底数．
    （1）当a=1时，求函数y=f（x）的单调区间；
    （2）求函数y=f（x）在区间[1，e]上的值域；
    （3）若a＞0，过原点分别作曲线y=f（x）、y=g（x）的切线l1、l2，且两切线的斜率互为倒数，求证：$\frac{e-1}{e}＜a＜\frac{{{e^2}-1}}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数$y=\frac{ln（2x-3）}{x-2}$的定义域是（　　）
    A．$[{\frac{3}{2}，+∞}）$B．$（{\frac{3}{2}，2}）∪（{2，+∞}）$C．$[{\frac{3}{2}，2}）∪（{2，+∞}）$D．（-∞，2）∪（2，+∞）

    查看答案和解析>>

    同步练习册答案