
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的普通方程;
(2)设直线l:2x+y-2=0与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
科目:高中数学 来源: 题型:
【题目】为了保护环境,某单位采用新工艺,把二氧化硅转化为一种可利用的化工产品.已知该单位每月都有处理量,且处理量最多不超过![]() 吨,月处理成本
吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一吨二氧化硅得到可利用的化工产品价值为
,且每处理一吨二氧化硅得到可利用的化工产品价值为![]() 元.
元.
(1)设该单位每月获利为![]() (元),试将
(元),试将![]() 表示月处理
表示月处理![]() (吨)的函数;
(吨)的函数;
(2)若要保证该单位每月不亏损,则每月处理量应控制在什么范围?
(3)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣2x﹣3,定义数列{ xn}如下:x1=2,xn+1是过两点P(4,5),Qn( xn , f(xn))的直线PQn与x轴交点的横坐标.
(1)证明:2≤xn<xn+1<3;
(2)求数列{ xn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
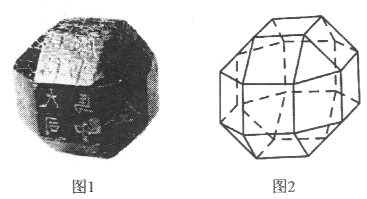
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体的所有棱长和为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C0: ![]() ,动圆C1:
,动圆C1: ![]() .点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
.点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2: ![]() 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com