
|
|
|
| 15×14 |
| 2 |
| 5×4 |
| 2 |
| 10×9 |
| 2 |
| n(n-1) |
| 2 |
| (15-n)(14-n) |
| 2 |


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源:0121 期末题 题型:解答题
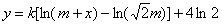 (其中k≠0);当燃料重量为
(其中k≠0);当燃料重量为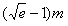 吨(e为自然对数的底数,e≈2.72)时,该火箭的最大速度为4km/s。
吨(e为自然对数的底数,e≈2.72)时,该火箭的最大速度为4km/s。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 每间房定价 | 100元 | 90元 | 80元 | 60元 |
| 住房率 | 65% | 75% | 85% | 95% |
| A.100元 | B.90元 | C.80元 | D.60元 |
查看答案和解析>>
科目:高中数学 来源:泰安二模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:崇明县二模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| k |
| m+1 |
| k |
| m+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com