
ЎѕМвДїЎїНЁ№эЛж»ъСЇОК110ГыґуС§ЙъКЗ·с°®єГДіПоФЛ¶ЇЈ¬µГµЅБРБЄ±нЈє
ДР | Е® | ЧЬјЖ | |
°®єГ | 40 | 20 | 60 |
І»°®єГ | 20 | 30 | 50 |
ЧЬјЖ | 60 | 50 | 110 |
УЙK2ЈЅ![]() Ј¬µГK2ЈЅ
Ј¬µГK2ЈЅ![]() ЎЦ7.8.
ЎЦ7.8.
ёЅ±нЈє
P(K2ЎЭk0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
ІОХХёЅ±нЈ¬µГµЅµДХэИ·ЅбВЫКЗ(ЎЎЎЎ)
A. УР99%ТФЙПµД°СОХИПОЄЎ°°®єГёГПоФЛ¶ЇУлРФ±рУР№ШЎ±
B. УР99%ТФЙПµД°СОХИПОЄЎ°°®єГёГПоФЛ¶ЇУлРФ±рОЮ№ШЎ±
C. ФЪ·ёґнОуµДёЕВКІ»і¬№э0.1%µДЗ°МбПВЈ¬ИПОЄЎ°°®єГёГПоФЛ¶ЇУлРФ±рУР№ШЎ±
D. ФЪ·ёґнОуµДёЕВКІ»і¬№э0.1%µДЗ°МбПВЈ¬ИПОЄЎ°°®єГёГПоФЛ¶ЇУлРФ±рОЮ№ШЎ±
 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЦ±ЅЗЧш±кПµЦРЈ¬ТФФµгОЄј«µгЈ¬ ![]() ЦбµДХэ°лЦбОЄј«ЦбЈ¬ТФПаН¬µДі¤¶ИµҐО»ЅЁБўј«Чш±кПµЈ¬ТСЦЄЦ±ПЯ
ЦбµДХэ°лЦбОЄј«ЦбЈ¬ТФПаН¬µДі¤¶ИµҐО»ЅЁБўј«Чш±кПµЈ¬ТСЦЄЦ±ПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() Ј¬ЗъПЯ
Ј¬ЗъПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() .
.
ЈЁ1Ј©Йи![]() ОЄІОКэЈ¬Иф
ОЄІОКэЈ¬Иф![]() Ј¬ЗуЦ±ПЯ
Ј¬ЗуЦ±ПЯ![]() µДІОКэ·ЅіМЈ»
µДІОКэ·ЅіМЈ»
ЈЁ2Ј©ТСЦЄЦ±ПЯ![]() УлЗъПЯ
УлЗъПЯ![]() Ѕ»УЪ
Ѕ»УЪ![]() Ј¬Йи
Ј¬Йи![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬ЗуКµКэ
Ј¬ЗуКµКэ![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©=|2x©Ѓ1|+|2x+3|Ј®
ЈЁ1Ј©ЅвІ»µИКЅfЈЁxЈ©ЎЭ6Ј»
ЈЁ2Ј©јЗfЈЁxЈ©µДЧоРЎЦµКЗmЈ¬ХэКµКэaЈ¬bВъЧг2ab+a+2b=mЈ¬Зуa+2bµДЧоРЎЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЅЗ![]() Кј±ЯУл
Кј±ЯУл![]() ЦбµД·Зёє°лЦбЦШєПЈ¬УлФІ
ЦбµД·Зёє°лЦбЦШєПЈ¬УлФІ![]() ПаЅ»УЪµг
ПаЅ»УЪµг![]() Ј¬ЦХ±ЯУлФІ
Ј¬ЦХ±ЯУлФІ![]() ПаЅ»УЪµг
ПаЅ»УЪµг![]() Ј¬µг
Ј¬µг![]() ФЪ
ФЪ![]() ЦбЙПµДЙдУ°ОЄ
ЦбЙПµДЙдУ°ОЄ![]() Ј¬
Ј¬ ![]() µДГж»эОЄ
µДГж»эОЄ![]() Ј¬єЇКэ
Ј¬єЇКэ![]() µДНјПуґуЦВКЗЈЁ Ј©
µДНјПуґуЦВКЗЈЁ Ј©
A. 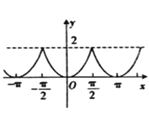 B.
B. 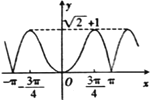
C. 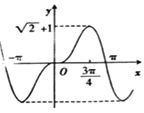 D.
D. 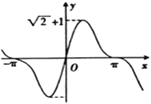
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЦ±ЅЗЧш±кПµЦРЈ¬ТФФµгОЄј«µгЈ¬xЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬ТСЦЄЗъПЯCЈє ![]() Ј¬№эµг
Ј¬№эµг![]() µДЦ±ПЯlµДІОКэ·ЅіМОЄЈє
µДЦ±ПЯlµДІОКэ·ЅіМОЄЈє 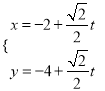 (tОЄІОКэ)Ј¬Ц±ПЯlУлЗъПЯC·Ц±рЅ»УЪMЎўNБЅµгЈ®
(tОЄІОКэ)Ј¬Ц±ПЯlУлЗъПЯC·Ц±рЅ»УЪMЎўNБЅµгЈ®
(ўс)РґіцЗъПЯCµДЦ±ЅЗЧш±к·ЅіМєНЦ±ПЯlµДЖХНЁ·ЅіМЈ»
(ўт)Иф| PM |Ј¬| MN |Ј¬| PN |іЙµИ±ИКэБРЈ¬ЗуaµДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіВГУОіЗКРОЄПтУОїНЅйЙЬ±ѕµШµДЖшОВЗйїцЈ¬»жЦЖБЛТ»ДкЦРёчФВЖЅѕщЧоёЯЖшОВєНЖЅѕщЧоµНЖшОВµДАЧґпНјЈ®НјЦРAµг±нКѕК®ФВµДЖЅѕщЧоёЯЖшОВФјОЄ15ЎжЈ¬Bµг±нКѕЛДФВµДЖЅѕщЧоµНЖшОВФјОЄ5ЎжЈ®ПВГжРрКцІ»ХэИ·µДКЗ ( )

A. ёчФВµДЖЅѕщЧоµНЖшОВ¶јФЪ0ЎжТФЙП
B. ЖЯФВµДЖЅѕщОВІо±ИТ»ФВµДЖЅѕщОВІоґу
C. ИэФВєНК®Т»ФВµДЖЅѕщЧоёЯЖшОВ»щ±ѕПаН¬
D. ЖЅѕщЧоёЯЖшОВёЯУЪ20ЎжµДФВ·ЭУР5ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиєЇКэ![]() ЈЁ
ЈЁ![]() Ј©µДНјПуОЄ
Ј©µДНјПуОЄ![]() Ј¬
Ј¬ ![]() №ШУЪµг
№ШУЪµг![]() µД¶ФіЖµДНјПуОЄ
µД¶ФіЖµДНјПуОЄ![]() Ј¬
Ј¬ ![]() ¶ФУ¦µДєЇКэОЄ
¶ФУ¦µДєЇКэОЄ![]() Ј®
Ј®
ЈЁўсЈ©ЗуєЇКэ![]() µДЅвОцКЅЈ¬ІўИ·¶ЁЖд¶ЁТеУтЈ»
µДЅвОцКЅЈ¬ІўИ·¶ЁЖд¶ЁТеУтЈ»
ЈЁўтЈ©ИфЦ±ПЯ![]() Ул
Ул![]() Ц»УРТ»ёцЅ»µгЈ¬Зу
Ц»УРТ»ёцЅ»µгЈ¬Зу![]() µДЦµЈ¬ІўЗуіцЅ»µгµДЧш±кЈ®
µДЦµЈ¬ІўЗуіцЅ»µгµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЎ°Л«К®Т»Ў±ЖЪјдЈ¬ДіМФ±¦µкЦч¶ФЖдЙМЖ·µДЙПјЬК±јд![]() ЈЁ·ЦЦУЈ©єНПъКЫБї
ЈЁ·ЦЦУЈ©єНПъКЫБї![]() ЈЁјюЈ©µД№ШПµЧчБЛНіјЖЈ¬µГµЅИзПВКэѕЭЈє
ЈЁјюЈ©µД№ШПµЧчБЛНіјЖЈ¬µГµЅИзПВКэѕЭЈє

ѕјЖЛгЈє ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() .
.
ЈЁ1Ј©ґУВъЧг![]() µДКэѕЭ
µДКэѕЭ![]() ЦРИОИЎБЅёцЈ¬ЗуЛщµГБЅёцКэѕЭ¶јВъЧг
ЦРИОИЎБЅёцЈ¬ЗуЛщµГБЅёцКэѕЭ¶јВъЧг![]() µДёЕВКЈ»
µДёЕВКЈ»
ЈЁ2Ј©ёГµкЦчНЁ№эЧчЙўµгНјЈ¬·ўПЦЙПјЬК±јдУлПъКЫБїПЯРФПа№ШЈ¬ЗлДг°пЦъµкЦчЗуіцЙПјЬК±јдУлПъКЫБїµДПЯРФ»Ш№й·ЅіМЈЁ±ЈБфИэО»РЎКэЈ©Ј¬ІўФ¤ІвЙМЖ·ЙПјЬ1000·ЦЦУК±µДПъКЫБї.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com