
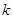 和
和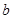 ,使得函数
,使得函数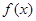 和
和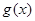 对其定义域上的任意实数
对其定义域上的任意实数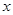 分别满足:
分别满足: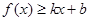 和
和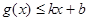 ,则称直线
,则称直线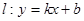 为
为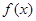 和
和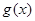 的“隔离直线”.已知
的“隔离直线”.已知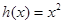 ,
,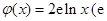 为自然对数的底数).
为自然对数的底数).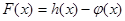 的极值;
的极值;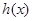 和
和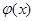 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. 时,
时, 取极小值,其极小值为
取极小值,其极小值为 (2)函数
(2)函数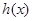 和
和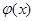 存在唯一的隔离直线
存在唯一的隔离直线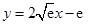

 ,
,  .
.  时,
时, .
.  当
当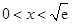 时,
时,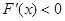 ,此时函数
,此时函数 递减;
递减;  时,
时,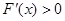 ,此时函数
,此时函数 递增;
递增; 时,
时, 取极小值,其极小值为
取极小值,其极小值为 . …………………………………6分
. …………………………………6分 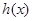 和
和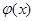 的图象在
的图象在 处有公共点,因此若存在
处有公共点,因此若存在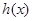 和
和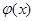 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点. 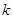 ,则直线方程为
,则直线方程为 ,即
,即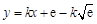 .
.  ,可得
,可得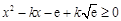 当
当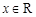 时恒成立.
时恒成立.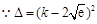 ,
,  由
由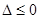 ,得
,得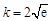 .
. 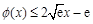 当
当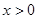 时恒成立.
时恒成立.
 ,则
,则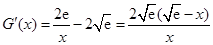 ,
, 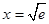 时,
时,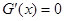 .
. 当
当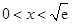 时,
时,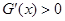 ,此时函数
,此时函数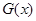 递增;
递增; 时,
时, ,此时函数
,此时函数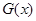 递减;
递减; 时,
时,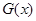 取极大值,其极大值为
取极大值,其极大值为 .
. 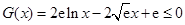 ,即
,即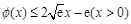 恒成立.
恒成立. 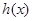 和
和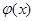 存在唯一的隔离直线
存在唯一的隔离直线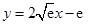 .……………12分
.……………12分 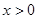 时,
时, (当且仅当
(当且仅当 时取等号) .
时取等号) . 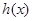 和
和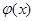 的隔离直线,则存在实常数
的隔离直线,则存在实常数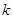 和
和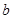 ,使得
,使得 和
和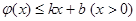 恒成立,
恒成立, ,则
,则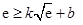 且
且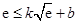
 ,即
,即 .
. 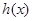 和
和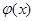 的图象在
的图象在 处有公共点是求解的关键
处有公共点是求解的关键

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
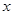 次之间的关系为Z=
次之间的关系为Z=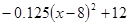 ,1≤
,1≤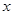 ≤16,且
≤16,且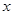 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元/千克,政府补贴为
元/千克,政府补贴为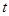 元/千克,根据市场调查,当
元/千克,根据市场调查,当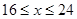 时,这种食品市场日供应量
时,这种食品市场日供应量 万千克与市场日需量
万千克与市场日需量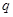 万千克近似地满足关系:
万千克近似地满足关系: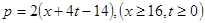 ,
, 。当
。当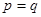 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
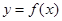 在区间(
在区间(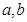 )的导函数
)的导函数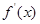 ,
,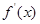 在区间(
在区间(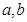 )的导函数
)的导函数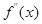 ,若在区间(
,若在区间(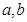 )上
)上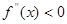 恒成立,则称函数
恒成立,则称函数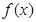 在区间(
在区间(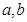 )为凸函数,已知
)为凸函数,已知 若当实数
若当实数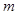 满足
满足 时,函数
时,函数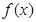 在
在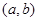 上为凸函数,则
上为凸函数,则 最大值 ( )
最大值 ( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com