
(本大题10分)求圆心在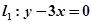 上,与
上,与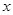 轴相切,且被直线
轴相切,且被直线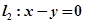 截得弦长为
截得弦长为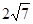 的圆的方程.
的圆的方程.
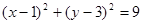 或
或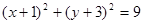 。
。
【解析】
试题分析:根据圆心在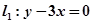 上,可设圆心坐标为(
上,可设圆心坐标为(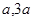 ),再根据它与
),再根据它与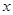 轴相切,得
轴相切,得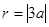 .
.
圆心到直线的距离等于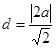 ,根据弦长公式可得
,根据弦长公式可得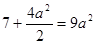 ,从而求出a的值,写出圆的标准方程.
,从而求出a的值,写出圆的标准方程.
由已知设圆心为(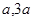 )--------1分
)--------1分
与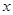 轴相切则
轴相切则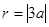 ---------2分
---------2分
圆心到直线的距离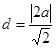 ----------3分
----------3分
弦长为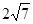 得:
得: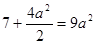 -------6分
-------6分
解得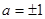 ---------7分
---------7分
圆心为(1,3)或(-1,-3),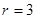 -----------8分
-----------8分
圆的方程为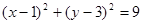 ---------9分
---------9分
或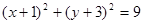 ----------10.
----------10.
考点:圆的标准方程.
点评:解本小题要利用点到直线的距离公式及圆的弦长公式:
点到直线的距离公式: 则
则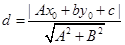 .
.
圆的弦长公式:弦长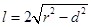 .
.


科目:高中数学 来源: 题型:
 (2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
(2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
|
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市二中学高三学情调查数学试卷 题型:解答题
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于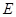 .
.
(1)求证: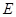 是
是 的中点;(2)求线段
的中点;(2)求线段 的长.
的长.
B.选修4-2:矩阵与变换
已知矩阵A ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
.
(1)求实数 的值;
的值;
(2)矩阵A的特征值和特征向量.
C. 选修4-4:坐标系与参数方程
在极坐标系中,圆 的极坐标方程为
的极坐标方程为 ,
,
(1)过极点的一条直线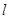 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长.
(2)求过圆上一点 ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程;
D.选修4-5:不等式选讲
已知实数 满足
满足 ,求
,求 的最小值;
的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
|
已知某圆的极坐标方程为![]()
(I)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(II)若点![]() 在该圆上,求
在该圆上,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题10分)选修4—4:坐标系与参数方程
已知某圆的极坐标方程为![]()
(I)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(II)若点![]() 在该圆上,求
在该圆上,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com