
����Ŀ��2018��4��23�ա���������ա�����֮�ʣ�ijУΪ���˽���ѧ�������Ķ�����������ȡ��100��ѧ���������������һ�ܿ����Ķ�ʱ�䣨��λ��Сʱ�������ݣ������õ����ݷ��鼰Ƶ���ֲ���.
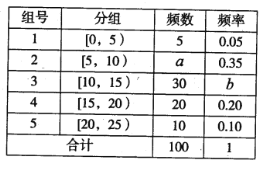
������![]() ��ֵ����������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
��ֵ����������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��

������ÿ�����������ƽ���ֲ��ģ��Թ��Ƹ������ݵ�ƽ��������ͬһ���е������ø���������е�ֵ����������
�����ִӵ�3��4��5�����÷ֲ�����ķ�����ȡ6�˲μ�У���л�ʫ�ʱ��������������������6����ѡ��2����ɸ�У�����ӣ�����2�����Բ�ͬ���ĸ���.
���𰸡������������������12.25������![]() .
.
��������
�����������ȼ���������͵������Ƶ�ʣ����������Ӧ���εĸߣ��ɵ�a��b��ֵ��
�����ۼӸ���Ƶ��������ֵ�ij˻����ɹ���ƽ������
�����ôӵ�3��4��5���ȡ�������ֱ�Ϊ3��2��1����Ϊ![]() ����������¼������Լ����Բ�ͬ�����Ļ����¼����������������.
����������¼������Լ����Բ�ͬ�����Ļ����¼����������������.
��⣺
����![]() ��
��![]()
Ƶ�ʷֲ�ֱ��ͼ����
�����Ƹ������ݵ�ƽ����
![]()
![]()
�����ôӵ�3��4��5���ȡ�������ֱ�Ϊ3��2��1����Ϊ![]() ����
����
�Ӹ�6����ѡ��2�˵Ļ����¼���![]() ��
��![]() ��15�֣��������Բ�ͬ�����Ļ����¼���
��15�֣��������Բ�ͬ�����Ļ����¼���![]() ��
��![]() ��11�֣�������2�����Բ�ͬ���ĸ���Ϊ
��11�֣�������2�����Բ�ͬ���ĸ���Ϊ![]() .����������������ͬ�飬������¼���
.����������������ͬ�飬������¼���![]() ��4�֣�������2�����Բ�ͬ���ĸ���Ϊ
��4�֣�������2�����Բ�ͬ���ĸ���Ϊ![]() .��
.��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���Զ�ͨ����ʩ.����ʩ���²�![]() �ǵ������Σ�����
�ǵ������Σ�����![]() Ϊ2�ף����εĸ�Ϊ1�ף�
Ϊ2�ף����εĸ�Ϊ1�ף� ![]() Ϊ3�ף��ϲ�
Ϊ3�ף��ϲ�![]() �Ǹ���Բ���̶���
�Ǹ���Բ���̶���![]() Ϊ
Ϊ![]() ���е�.
���е�. ![]() ���ɵ��Կ��ƿ������»�����������ˣ��������ɺ��Բ��ƣ����һ���������ʼ�ձ��ֺ�
���ɵ��Կ��ƿ������»�����������ˣ��������ɺ��Բ��ƣ����һ���������ʼ�ձ��ֺ�![]() ƽ��.��
ƽ��.��![]() λ��
λ��![]() �·����Ϸ�ʱ��ͨ�細����״��Ϊ����
�·����Ϸ�ʱ��ͨ�細����״��Ϊ����![]() ����Ӱ���־���ͨ�磩.
����Ӱ���־���ͨ�磩.
��1����![]() ��
��![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ��
��![]() ��
��![]() ���ף��Խ�ͨ�細��ͨ�����
���ף��Խ�ͨ�細��ͨ�����![]() ��ƽ���ף���ʾ�ɹ���
��ƽ���ף���ʾ�ɹ���![]() �ĺ���
���![]() ��
��
��2����![]() ��
��![]() ֮��ľ���Ϊ������ʱ��ͨ�細��ͨ�����
֮��ľ���Ϊ������ʱ��ͨ�細��ͨ�����![]() ȡ�����ֵ��
ȡ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ���һ��������������һ���齱��Ϸ.�齱���й���12��ֽ������һ�Ƚ������Ƚ������Ƚ���������.������ȡһ�ţ����н��ĸ���Ϊ![]() ���ж��Ƚ������Ƚ��ĸ�����
���ж��Ƚ������Ƚ��ĸ�����![]() .
.
����������ȡһ�ţ���һ�Ƚ��ĸ��ʣ�
����������һ�Ƚ�����Ƚ��ĸ�����![]() ������ȡһ���������Ƚ��ĸ���.
������ȡһ���������Ƚ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABC��,BC���ϵĸ�AM���ڵ�ֱ�߷���Ϊx-2y+1=0,��A��ƽ�������ڵ�ֱ�߷���Ϊy=0��BC�ཻ�ڵ�P,����B������Ϊ(1,2).

(1)�ֱ���AB��BC����ֱ�ߵķ���;
(2)��P�������AC����ֱ�ߵķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˹涨��ʱ�����Ҫȷ���ӹ���������ѵ�ʱ�䣬Ϊ�������Ĵ����飬�õ����������£�
����ĸ���x������ | 2 | 3 | 4 | 5 |
�ӹ���ʱ��y��Сʱ�� | 2.5 | 3 | 4 | 4.5 |

��1���ڸ���������ϵ�л����������ݵ�ɢ��ͼ��
��2�����y����x�����Իع鷽��![]() ��bx��a��
��bx��a��
��3����Ԥ��ӹ�20�������Ҫ����Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��k��R����
��k��R����
��1������y=f��x���ĵ������䣻
��2����k��N*���ҵ�x�ʣ�1��+�ޣ�ʱ��f��x����0���������k�����ֵ���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|������a��1
��1����a=2ʱ����ʽf��x����4��|x��4|�Ľ⼯��
��2����֪����x�IJ���ʽ|f��2x+a����2f��x��|��2�Ľ⼯{x|1��x��2}����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1������![]() �ڵ�
�ڵ�![]() �㴦�����߷��̣�
�㴦�����߷��̣�
��2����![]() ʱ������
ʱ������![]() �ļ�ֵ��ͼ�ֵ��
�ļ�ֵ��ͼ�ֵ��
��3����![]() ʱ��
ʱ�� ![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�����C1�IJ�������Ϊ ![]() ����Ϊ������������C2�IJ�������Ϊ
����Ϊ������������C2�IJ�������Ϊ ![]() ����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ��
����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���Ὠ��������ϵ��
��1��������C1������C2�ļ����귽�̣�
��2����֪����l1����=���� ![]() ������
������ ![]() ����������l1˳ʱ�뷽����ת
����������l1˳ʱ�뷽����ת ![]() �õ�l2����=����
�õ�l2����=���� ![]() ��������l1������C1�������㣬����l2������C2����O��Q���㣬��|OP||OQ|�����ֵ��
��������l1������C1�������㣬����l2������C2����O��Q���㣬��|OP||OQ|�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com