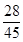在10件产品中有2件次品,连续抽3次,每次抽1件,
求:(1)不放回抽样时,抽到次品数ξ的分布列;
(2)放回抽样时,抽到次品数η的分布列.
分析:(1)由题意知随机变量ξ可以取0,1,2,当ξ=0时表示没有抽到次品,当ξ=1时表示抽到次品数是一个,ξ=2时表示抽到次品数是两个根据古典概型公式得到概率,写出分布列.
(2)由题意知放回抽样时,每一次抽样可以作为一次实验,抽到次品的概率是相同的,且每次试验之间是相互独立的,得到η~B(3,0.8).后面可以根据二项分布得到结果.
解答:解:(1)由题意知随机变量ξ可以取0,1,2,
∵当ξ=0时表示没有抽到次品,
∴P(ξ=0)=
=
,
∵当ξ=1时表示抽到次品数是一个,
∴P(ξ=1)=
=
,
∵ξ=2时表示抽到次品数是两个
∴P(ξ=2)=
=
,
∴ξ的分布列为

(2)η也可以取0,1,2,3,
∵由题意知放回抽样时,每一次抽样可以作为一次实验,
抽到次品的概率是相同的,
且每次试验之间是相互独立的,
∴η~B(3,0.8).
∴P(η=k)=C
8k•0.8
3-k•0.2
k(k=0,1,2,3),
∴η的分布列为

点评:放回抽样和不放回抽样对随机变量的取值和相应的概率都产生了变化,要具体问题具体分析.放回抽样时,抽到的次品数为独立重复试验事件,即η~B(3,0.8).





 全能测控期末小状元系列答案
全能测控期末小状元系列答案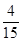 B.
B.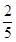 C.
C. D.
D.