
| 男 | 女 | |
| 喜欢数学 | 7 | 3 |
| 不喜欢数学 | 3 | 7 |
 ,
,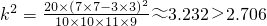
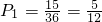 ;
; .…(12分)
.…(12分)

科目:高中数学 来源: 题型:
| 男 | 女 | |
| 喜欢数学 | 7 | 3 |
| 不喜欢数学 | 3 | 7 |
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
查看答案和解析>>
科目:高中数学 来源:安徽省六安一中2012届高三第十次月考数学文科试题 题型:044
为了调查高中学生是否喜欢数学与性别的关系,某班采取分层抽样的方法从2011届高一学生中随机抽出20名学生进行调查,具体情况如下表所示.
(Ⅰ)用独立性检验的方法分析有多大的把握认为本班学生是否喜欢数学与性别有关?(参考公式和数据:(1)k2=![]() ,(2)①当k2≤2.706时,可认为两个变量是没有关联的;②当k2>2.706时,有90%的把握判定两个变量有关联;③当k2>3.841时,有95%的把握判定两个变量有关联;④当k2>6.635时,有99%的把握判定两个变量有关联.)
,(2)①当k2≤2.706时,可认为两个变量是没有关联的;②当k2>2.706时,有90%的把握判定两个变量有关联;③当k2>3.841时,有95%的把握判定两个变量有关联;④当k2>6.635时,有99%的把握判定两个变量有关联.)
(Ⅱ)若按下面的方法从这个20个人中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,试求:①抽到号码是6的倍数的概率;②抽到“无效序号(序号大于20)”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com