
分析 连接OA、OE、OB,OB交⊙O于点P,此时BP+$\frac{\sqrt{2}}{2}$AP的值最小;由⊙O是正方形ABCD的内切圆得出BE=OE=OP=$\frac{1}{2}$BC=1,OE⊥BC,OA⊥OB,OB=OA=$\sqrt{2}$BE=$\sqrt{2}$,得出BP,由勾股定理求出AP,即可得出结果.
解答 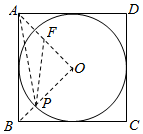 解:如图所示:
解:如图所示:
取AO的中点F
所以$\frac{PO}{FO}$=$\frac{AO}{PO}$=$\sqrt{2}$,又∠POF=∠AOP
所以△POF~△AOP
所以PF=$\frac{\sqrt{2}}{2}$AP,
所以F,P,B三点共线时BP+$\frac{\sqrt{2}}{2}$AP取最小值为$\frac{\sqrt{10}}{2}$.
所以$\sqrt{2}$(BP+$\frac{\sqrt{2}}{2}$AP)=$\sqrt{2}$•$\frac{\sqrt{10}}{2}$=$\sqrt{5}$
点评 本题考查了正方形的性质、正方形的内切圆的性质、勾股定理、等腰直角三角形的性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 1 101 101 | B. | 11 011 011 | C. | 1 101 111 | D. | 1 011 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}-\sqrt{3}}{6}$ | B. | $\frac{2\sqrt{2}+\sqrt{3}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{2}}{6}$ | D. | $\frac{2\sqrt{3}+\sqrt{2}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com