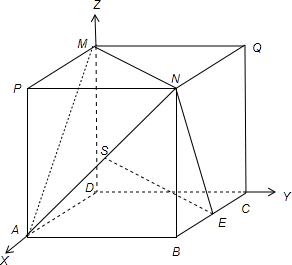
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?
(3)若存在,求线段AS的长;若不存在,请说明理由.
分析:(1)以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,建立空间坐标系,分别求出各点的坐标,进而求出直线NE与AM的方向向量,代入向量夹角公式,即可得到答案.;
(2)连接PB,交AN与S,连接SE,则易得S为PB的中点,又由E为BC的中点,由三角形中位线的性质,结合ES⊥平面AMN,易得线段AN上存在一点S为AN的中点,满足ES⊥平面AMN
(3)由(2)的结论,我们易求出S点的坐标,代入空间中两点之间距离公式,即可得到答案.本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,
解答:解:∵MD⊥平面ABCD,则MD⊥DA,MD⊥DC,
又∵底面ABCD为正方形,∴DA⊥DC,
故以点D为坐标原点,DA为x轴,DC为y轴,DM为z轴,如图建立空间直角坐标系.
则各点的坐标D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),E,(
,1,0),M(0,0,1),N(1,1,1),
(1)∴
=(-
,0,-1),
=(-1,0,1)
设异面直线NE与AM所成角为θ
则cosθ=
||=
=
故异面直线NE与AM所成角的余弦值为
(2)由正方体的几何特征,我们易得PC⊥平面AMN
连接PB,交AN与S,连接SE,则易得S为PB的中点,又由E为BC的中点
则SE∥PC
∴ES⊥平面AMN
即线段AN上存在一点S为AN的中点,满足ES⊥平面AMN
(3)由(2)得,S的坐标为(1,
,
)
则线段AS的长d=
AN=
点评:在判断空间线面的关系,常常把他们放在空间几何体中来直观的分析,在判断线与面的平行与垂直关系时,正方体是最常用的空间模型,大家一定要熟练掌握这种方法.另外熟练掌握线线、线面、面面平行(或垂直)的判定及性质定理是解决此类问题的基础.




 科学实验活动册系列答案
科学实验活动册系列答案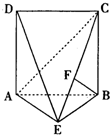 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE. 如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,
如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1, (2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点,点Q在AB上,且BQ=
(2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点,点Q在AB上,且BQ=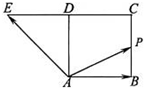 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,