
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的
个单位长度,再将图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象.求证:存在无穷多个互不相同的整数
的图象.求证:存在无穷多个互不相同的整数![]() ,使得
,使得![]() .
.
【答案】(1)单调递增区间为![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)利用二倍角的降幂公式以及辅助角公式可将函数![]() 的解析式化简为
的解析式化简为![]() ,然后求出函数
,然后求出函数![]() 在
在![]() 上的单调递增区间
上的单调递增区间![]() ,与定义域取交集可得出答案;
,与定义域取交集可得出答案;
(2)利用三角函数图象变换得出![]() ,解出不等式
,解出不等式![]() 的解集
的解集![]() ,可得知对
,可得知对![]() 中的任意一个
中的任意一个![]() ,每个区间
,每个区间![]() 内至少有一个整数
内至少有一个整数![]() 使得
使得![]() ,从而得出结论.
,从而得出结论.
(1)![]()
![]() .
.
令![]() ,解得
,解得![]() ,
,
所以,函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]() ,
,
![]() ,因此,函数
,因此,函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]() ;
;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,
的图象,
再将图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,
的图象,
由![]() ,
,
对于![]() 中的任意一个
中的任意一个![]() ,区间
,区间![]() 长度始终为
长度始终为![]() ,大于
,大于![]() ,
,
![]() 每个区间
每个区间![]() 至少含有一个整数,
至少含有一个整数,
因此,存在无穷多个互不相同的整数![]() ,使得
,使得![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为![]() (
(![]() 为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)过点![]() ,倾斜角为
,倾斜角为![]() 的直线l与曲线C相交于M,N两点,求
的直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之和为
的距离之和为![]() .
.
(1)求点![]() 的轨迹方程,并在答题卡所示位置画出方程的曲线草图;
的轨迹方程,并在答题卡所示位置画出方程的曲线草图;
(2)(理)记(1)得到的轨迹为曲线![]() ,问曲线
,问曲线![]() 上关于点
上关于点![]() 对称的不同点有几对?请说明理由.
对称的不同点有几对?请说明理由.
(3)(文)记(1)得到的轨迹为曲线![]() ,若曲线
,若曲线![]() 上恰有三对不同的点关于点
上恰有三对不同的点关于点![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时乘船出发,以匀速![]() 海里/小时
海里/小时![]() 从
从![]() 港前往相距50海里的
港前往相距50海里的![]() 港,然后乘汽车以匀速
港,然后乘汽车以匀速![]() 千米/小时(
千米/小时(![]() )自
)自![]() 港前往相距
港前往相距![]() 千米的
千米的![]() 市,计划当天下午4到9时到达
市,计划当天下午4到9时到达![]() 市.设乘船和汽车的所要的时间分别为
市.设乘船和汽车的所要的时间分别为![]() 、
、![]() 小时,如果所需要的经费
小时,如果所需要的经费![]() (单位:元)
(单位:元)

(1)试用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
(2)要使得所需经费![]() 最少,求
最少,求![]() 和
和![]() 的值,并求出此时的费用.
的值,并求出此时的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() ,对任意
,对任意![]() 都有
都有![]() ,(其中k、b、p是常数).
,(其中k、b、p是常数).
(1)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ;
;
(2)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当![]() ,
,![]() ,
,![]() 时,设
时,设![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,试问:是否存在这样的“封闭数列”
,试问:是否存在这样的“封闭数列”![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求数列
.若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由.
的所有取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面为正方形,![]()
![]() ,AC与BD交于E,M,N分别为SD,SA的中点,
,AC与BD交于E,M,N分别为SD,SA的中点,![]() .
.
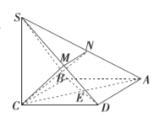
(1)求证:平面![]() 平面SBD;
平面SBD;
(2)求直线BD与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用![]() 模式,其中语文、数学、外语三科为必考科目,每门科目满分均为
模式,其中语文、数学、外语三科为必考科目,每门科目满分均为![]() 分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每门科目满分均为
),每门科目满分均为![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取
人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查,其中,女生抽取
名学生进行调查,其中,女生抽取![]() 人.
人.
(1)求![]() 的值;
的值;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的![]() 名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的
名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的![]() 列联表,请将下面的
列联表,请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“地理” | 总计 | |
男生 |
| ||
女生 |
| ||
总计 |
(3)在抽取到的![]() 名女生中,按(2)中的选课情况进行分层抽样,从中抽出
名女生中,按(2)中的选课情况进行分层抽样,从中抽出![]() 名女生,再从这
名女生,再从这![]() 名女生中抽取
名女生中抽取![]() 人,设这
人,设这![]() 人中选择“物理”的人数为
人中选择“物理”的人数为![]() ,求
,求![]() 的分布列及期望.附:
的分布列及期望.附:![]() ,
,![]()
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
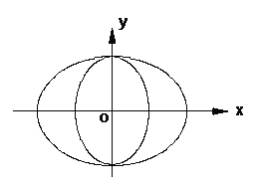
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.
为“猫眼曲线”.
(1)若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() ,求猫眼曲线
,求猫眼曲线![]() 的方程;
的方程;
(2)对于题(1)中的求猫眼曲线![]() ,任作斜率为
,任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为M,交椭圆
所得弦的中点为M,交椭圆![]() 所得弦的中点为N,求证:
所得弦的中点为N,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com