
【题目】已知椭圆C1:![]() y2=1的左右顶点是双曲线C2:
y2=1的左右顶点是双曲线C2:![]() 的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为
的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为![]() .
.
(1)求双曲线C2的方程;
(2)若直线与C1相交于M1,M2两点,与C2相交于Q1,Q2两点,且![]()
![]() 5,求|M1M2|的取值范围.
5,求|M1M2|的取值范围.
【答案】(1)![]() y2=1;(2)|M1M2|∈(0,
y2=1;(2)|M1M2|∈(0,![]() ].
].
【解析】
(1)由椭圆的顶点可得![]() ,求出双曲线的渐近线方程,运用点到直线的距离公式可得
,求出双曲线的渐近线方程,运用点到直线的距离公式可得![]() ,进而得到双曲线的方程;
,进而得到双曲线的方程;
(2)设出直线![]() 的方程,联立双曲线方程,消去
的方程,联立双曲线方程,消去![]() ,运用韦达定理和判别式大于0,结合向量的数量积的坐标运算,求得
,运用韦达定理和判别式大于0,结合向量的数量积的坐标运算,求得![]() 的关系式,再由直线方程和椭圆的方程联立,运用韦达定理和弦长公式,即可求得
的关系式,再由直线方程和椭圆的方程联立,运用韦达定理和弦长公式,即可求得![]() 的取值范围.
的取值范围.
(1)由椭圆C1:![]() y2=1的左右顶点为(
y2=1的左右顶点为(![]() ,0),(
,0),(![]() ,0),可得a2=3,
,0),可得a2=3,
又椭圆C1的上顶点(0,1)到双曲线C2的渐近线bx﹣ay=0的距离为![]() ,
,
由点到直线的距离公式有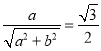 可得b=1,
可得b=1,
所以双曲线C2的方程为![]() y2=1;
y2=1;
(2)易知直线l的斜率存在,设直线l的方程为y=kx+m,
代入![]() y2=1,消去y并整理得(1﹣3k2)x2﹣6kmx﹣3m2﹣3=0,
y2=1,消去y并整理得(1﹣3k2)x2﹣6kmx﹣3m2﹣3=0,
要与C2相交于两点,则应有
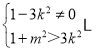 ①,
①,
设Q1(x1,y1)、Q2(x2,y2),则有:x1+x2![]() ,x1x2
,x1x2![]() .
.
又![]()
![]() x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2,
x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2,
又![]()
![]() 5,所以有
5,所以有![]() [(1+k2)(﹣3m2﹣3)+6k2m2+m2(1﹣3k2)]=﹣5
[(1+k2)(﹣3m2﹣3)+6k2m2+m2(1﹣3k2)]=﹣5
整理得m2=1﹣9k2…②,
将y=kx+m,代入![]() y2=1,消去y并整理得:(1+3k2)x2+6kmx+3m2﹣3=0,
y2=1,消去y并整理得:(1+3k2)x2+6kmx+3m2﹣3=0,
要有两交点,则△=36k2m2﹣4(1+3k2)(3m2﹣3)>03k2+1>m2…③
由①②③有:0<k2![]() .
.
设M1(x3,y3)、M2(x4,y4),则有:x3+x4![]() ,x3x4
,x3x4![]() .
.
所以|M1M2|![]()

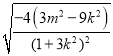 ,
,
又m2=1﹣9k2,代入有:|M1M2|![]()
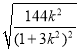 |M1M2|
|M1M2|![]()
![]()
|M1M2|=12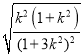 ,令t=k2,则
,令t=k2,则![]() ],
],
令f(t)![]() f′(t)
f′(t)![]() ,又t∈(0,
,又t∈(0,![]() ],
],
所以f'(t)>0在t∈(0,![]() ]内恒成立,故函数f(t)在t∈(0,
]内恒成立,故函数f(t)在t∈(0,![]() ]内单调递增,
]内单调递增,
故f(t)∈(0,![]() ],则有|M1M2|∈(0,
],则有|M1M2|∈(0,![]() ].
].


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
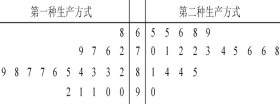
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
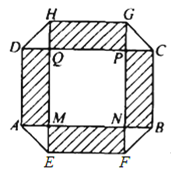
【题目】如图,居民小区要建一座八边形的休闲场所,它的主体造型平面图是由两个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() 的十字形地域,计划在正方形
的十字形地域,计划在正方形![]() 上建一座花坛,造价为
上建一座花坛,造价为![]() 元/
元/![]() ;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为
;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为![]() 元/
元/![]() ;再在四个空角(图中四个三角形,如
;再在四个空角(图中四个三角形,如![]() )上铺草坪,造价为
)上铺草坪,造价为![]() 元/
元/![]()
(1)设总造价为![]() (单位:元),
(单位:元),![]() 长为
长为![]() (单位:
(单位:![]() ),试求出
),试求出![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)当![]() 长
长![]() 取何值时,总造价
取何值时,总造价![]() 最小,并求出这个最小值.
最小,并求出这个最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]()
![]() 的焦距为
的焦距为![]() ,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
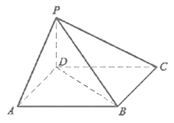
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马.如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.
(1)若![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长(精确到
的长(精确到![]() );
);
(2)证明:四面体![]() 为鳖臑;
为鳖臑;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一个动点,求
上一个动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元;未售出的产品,每盒亏损30元![]() 根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以
根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以![]() 单位:盒,
单位:盒,![]() 表示这个开学季内的市场需求量,
表示这个开学季内的市场需求量,![]() 单位:元
单位:元![]() 表示这个开学季内经销该产品的利润
表示这个开学季内经销该产品的利润
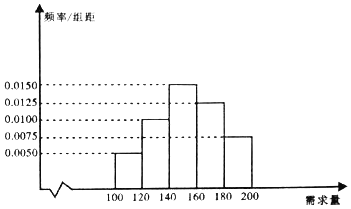
![]() 根据直方图估计这个开学季内市场需求量x的平均数和众数;
根据直方图估计这个开学季内市场需求量x的平均数和众数;
![]() 将y表示为x的函数;
将y表示为x的函数;
![]() 根据直方图估计利润不少于4800元的概率.
根据直方图估计利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com