
(14分)直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B.
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(1)-2<k<- .(2) k=-
.(2) k=- .
.
【解析】(1)直线与双曲线方程联立消y得关于x的一元二次方程,根据判别式大于零,可求出k的取值范围.
(2) 解本题的突破口是假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得(x1-c)(x2-c)+y1y2=0,即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0,
整理得:(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0再根据韦达定理解决即可.
(1)将直线l的方程y=kx+1代入双曲线方程2x2-y2=1后,整理得:
(k2-2)x2+2kx+2=0①
解:依题意,直线l与双曲线C的右支交于不同两点,故
 ,解得-2<k<-
,解得-2<k<- .
.
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),则由①式得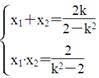 ②,
②,
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得(x1-c)(x2-c)+y1y2=0,即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0,
整理得:(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0③
把②式及c=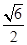 代入③式化简得5k2+2
代入③式化简得5k2+2 k-6=0,解得
k-6=0,解得
k=- 或k=
或k=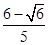 ∉(-2,-
∉(-2,- )(舍去).
)(舍去).
可得k=- 使得以线段AB为直径的圆经过双曲线C的右焦点.
使得以线段AB为直径的圆经过双曲线C的右焦点.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 季度 | 1 | 2 | 3 | 4 |
| x | 30 | 31 | 33 | 34 |
| y | 18 | 16 | 14 | 12 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中四模理)( 14分)
直线l:ax-y-1=0与曲线C:x2-2y2=1交于P、Q两点,
(1)当实数a为何值时,|PQ|=2![]() .
.
(2)是否存在a的值,使得以PQ为直径的圆经过原点?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com