
(本小题12分) 定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)= x0,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ 对称,求b的最小值.
对称,求b的最小值.
(1)-1或3;(2)0<a<1;(3)bmin=-1
【解析】(1)f(x)=x2-x-3,由x2-x-3=x,解得 x=3或-1,
所以所求的不动点为-1或3. ………………………3分
(2)令ax2+(b+1)x+b-1=x,则ax2+bx+b-1=0 ①
由题意,方程①恒有两个不等实根,所以△=b2-4a(b-1)>0,
即b2-4ab+4a>0恒成立,………………………………5分
则△¢=16a2-16a<0,故0<a<1 …………………………7分[来源:学+科+网Z+X+X+K]
(3)设A(x1,x1),B(x2,x2)(x1≠x2),则kAB=1,∴k=﹣1,
所以y=-x+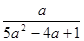 ,
……………………………………8分
,
……………………………………8分
又AB的中点在该直线上,所以=﹣+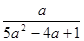 ,
,
∴x1+x2=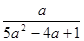 ,
,
而x1、x2应是方程①的两个根,所以x1+x2=﹣,即﹣=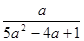 ,
,
∴b=﹣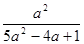 …………………………………………10分
…………………………………………10分
=-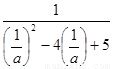 =-
=-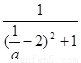
∴当 a=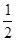 ∈(0,1)时,bmin=-1
.………………………………12分
∈(0,1)时,bmin=-1
.………………………………12分


科目:高中数学 来源: 题型:
(本小题12分)设点![]() ,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足
,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足![]() ,
,![]() .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)设轨迹C的焦点为F,准线为l,自M引的垂线,垂足为N,设点![]() 使四边形PFMN是菱形,试求实数a;
使四边形PFMN是菱形,试求实数a;
 (Ⅲ)如果点A的坐标为
(Ⅲ)如果点A的坐标为![]() ,
,![]() ,其中
,其中![]() >
>![]() ,相应线段AM的垂直平分线交x轴于
,相应线段AM的垂直平分线交x轴于![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,证明:当n≥2时,
,证明:当n≥2时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
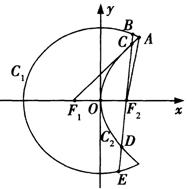
如图,曲线![]() 是以原点
是以原点![]() 为中心,以
为中心,以![]() 、
、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以
是以![]() 为顶点,以
为顶点,以![]() 为焦点的抛物线的一部分,
为焦点的抛物线的一部分,![]() 是曲线
是曲线![]() 和
和![]() 的交点,且
的交点,且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.
(I)求曲线![]() 和
和![]() 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过![]() 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线![]() 、
、![]() 依次交于
依次交于![]() 、
、![]() 、
、![]() 、
、![]() 四点(如图),若
四点(如图),若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,问
的中点,问![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)已知椭圆C的焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率
的焦点,离心率![]() 。(1)求椭圆的标准方程
。(1)求椭圆的标准方程![]() ;(2)过椭圆C的右焦点
;(2)过椭圆C的右焦点![]() 作直线
作直线![]() 交椭圆C于A、B两点,交y轴于M,若
交椭圆C于A、B两点,交y轴于M,若![]() 为定值吗?证明你的结论。
为定值吗?证明你的结论。
查看答案和解析>>
科目:高中数学 来源:浏阳一中、田中高三年级2009年下期期末联考试题 数学试题 题型:解答题
(本小题12分)
如图,曲线 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 为顶点,以
为顶点,以 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线 和
和 的交点,且
的交点,且 为钝角,若
为钝角,若 ,
, .
.
(I)求曲线 和
和 所在的椭圆和抛物线的方程;
所在的椭圆和抛物线的方程;
(II)过 作一条与轴不垂直的直线,分别与曲线
作一条与轴不垂直的直线,分别与曲线 、
、 依次交于
依次交于 、
、 、
、 、
、 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省石家庄市毕业班复习质量检测数学理卷 题型:解答题
(本小题12分)
已知动点P到定点A(0,1)的距离比它到定直线y = -2的距离小1.
(I)求动点P的轨迹C的方程;
(II)已知点Q为直线y= -1上的动点,过点q作曲线C的两条切线,切点分别为M,N,求 的取值范围.(其中O为坐标原点)
的取值范围.(其中O为坐标原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com