
分析 由题意把$\overrightarrow{HF}$、$\overrightarrow{HD}$用向量$\overrightarrow{AB}、\overrightarrow{AC}$表示,展开数量积可得关于λ的方程,则答案可求.
解答 解:如图,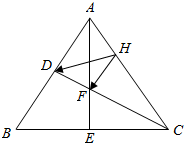
由题意可知,F为三角形ABC的重心,
$\overrightarrow{HF}=\overrightarrow{AF}-\overrightarrow{AH}=\frac{2}{3}\overrightarrow{AE}-λ\overrightarrow{AC}=\frac{2}{3}$×$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$$-λ\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AB}+(\frac{1}{3}-λ)\overrightarrow{AC}$,
$\overrightarrow{HD}=\overrightarrow{AD}-\overrightarrow{AH}=\frac{1}{2}\overrightarrow{AB}-λ\overrightarrow{AC}$,
由$\overrightarrow{HF}$•$\overrightarrow{HD}$=$[\frac{1}{3}\overrightarrow{AB}+(\frac{1}{3}-λ)\overrightarrow{AC}]•(\frac{1}{2}\overrightarrow{AB}-λ\overrightarrow{AC})$=$\frac{1}{6}|\overrightarrow{AB}{|}^{2}-λ(\frac{1}{3}-λ)|\overrightarrow{AC}{|}^{2}$$+(\frac{1}{6}-\frac{5}{6}λ)\overrightarrow{AB}•\overrightarrow{AC}$=1,得
$\frac{1}{6}×4-4λ(\frac{1}{3}-λ)+$$(\frac{1}{6}-\frac{5}{6}λ)×2=1$,整理得:4λ2-3λ=0,
∵0<λ<1,∴$λ=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查平面向量的数量积运算,考查了平面向量的加减法,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )| A. | $\frac{18+9\sqrt{3}}{2}$ | B. | 18+9$\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | D. | $y=x+\frac{1}{4(x-2)}-1(x>2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com