
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为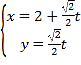 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 随机地填入图正方形ABCD的九个格子中,每格填一数,则其每列三数自上而下、每行三数自左至右顺次成等差数列的概率P=____________.
随机地填入图正方形ABCD的九个格子中,每格填一数,则其每列三数自上而下、每行三数自左至右顺次成等差数列的概率P=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为an=n2-n-30.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:

(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取3人,设
的学生中任取3人,设![]() 表示这3人中成绩满足
表示这3人中成绩满足![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据以往培训数据,规定当![]() 时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级学生为了庆祝教师节,同学们为老师制作了一大批同一种规格的手工艺品,这种工艺品有![]()
![]() 两项技术指标需要检测,设各项技术指标达标与否互不影响,若
两项技术指标需要检测,设各项技术指标达标与否互不影响,若![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() ,按质量检验规定:两项技术指标都达标的工艺品为合格品.
,按质量检验规定:两项技术指标都达标的工艺品为合格品.
(1)求一个工艺品经过检测至少一项技术指标达标的概率;
(2)任意依次抽取该工艺品4个,设![]() 表示其中合格品的个数,求
表示其中合格品的个数,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com